本试题 “如图,在直三棱柱ABC-A1B1C1中,侧面ABB1A1是边长为2的正方形,AC=BC,E为A1C上的点,且AE⊥平面A1CB,(Ⅰ)求证:BC⊥平面AA1C;(Ⅱ)求三棱锥B1-A1CB的体积。” 主要考查您对柱体、椎体、台体的表面积与体积
直线与平面垂直的判定与性质
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 柱体、椎体、台体的表面积与体积
- 直线与平面垂直的判定与性质
侧面积和全面积的定义:
(1)侧面积的定义:把柱、锥、台的侧面沿着它们的一条侧棱或母线剪开,所得到的展开图的面积,就是空间几何体的侧面积.
(2)全面积的定义:空间几何体的侧面积与底面积的和叫做空间几何体的全面积,
柱体、锥体、台体的表面积公式(c为底面周长,h为高,h′为斜高,l为母线)
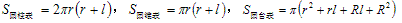
柱体、锥体、台体的体积公式:

多面体的侧面积与体积:
| 多面体 | 图像 | 侧面积 | 体积 |
| 棱柱 |
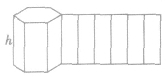 |
直棱柱的侧面展开图是矩形 |
 |
| 棱锥 |
 |
正棱柱的侧面展开图是一些全等的等腰三角形,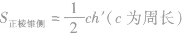 |
 |
| 棱台 |
 |
正棱台的侧面展开图是一些全等的等腰梯形,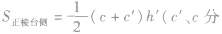  |
 |
旋转体的侧面积和体积:
| 旋转体 | 图形 | 侧面积与全面积 | 体积 |
| 圆柱 |
 |
圆柱的侧面展开图的矩形: |
 |
| 圆锥 |
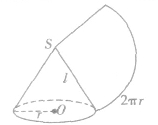 |
圆锥的侧面展开图是扇形: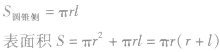 |
 |
| 圆台 |
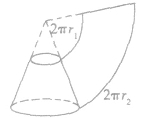 |
圆台的侧面展开图是扇环: |
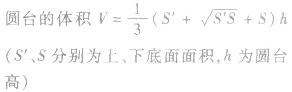 |
| 球 |
 |
 |
 |
线面垂直的定义:
如果一条直线l和一个平面α内的任何一条直线垂直,就说这条直线l和这个平面α互相垂直,记作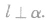 直线l叫做平面α的垂线,平面α叫做直线l的垂面。直线与平面垂直时,它们唯一的公共点P叫做垂足。
直线l叫做平面α的垂线,平面α叫做直线l的垂面。直线与平面垂直时,它们唯一的公共点P叫做垂足。
线面垂直的画法:
画线面垂直时,通常把直线画成与表示平面的平行四边形的一边垂直,如图所示:
线面垂直的判定定理:
如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直这个平面。(线线垂直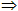 线面垂直)
线面垂直)
符号表示:
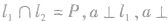
 如图所示,
如图所示,
线面垂直的性质定理:
如果两条直线同垂直于一个平面,那么这两条直线平行。
(线面垂直 线线平行)
线线平行)
线面垂直的判定定理的理解:
(1)判定定理的条件中,“平面内的两条相交直线”是关键性语句,一定要记准.
(2)如果一条直线垂直于平面内的两条直线,那么这条直线垂直于这个平面,这个结论是错误的.
(3)如果一条直线垂直于平面内的无数条直线,那么这条直线垂直于这个平面,这个结论也错误,因为这无数条直线可能平行.
证明线面垂直的方法:
(1)线面垂直的定义拓展了线线垂直的范围,线垂直于面,线就垂直于面内所有直线,这也是线面垂直的必备条件,利用这个条件可将线线垂直与线面垂直互相转化,这样就完成了空间问题与平面问题的转化.
(2)证线面垂直的方法①利用定义:若一直线垂直于平面内任一直线,则这条直线垂直于该平面.②利用线面垂直的判定定理:证一直线与一平面内的两条相交直线都垂直,③利用线面垂直的性质:两平行线中的一条垂直于平面,则另一条也垂直于这个平面,④用面面垂直的性质定理:两平面垂直,在一个平面内垂直于交线的直线必垂直于另一个平面.⑤用面面平行的性质定理:一直线垂直于两平行平面中的一个,那么它必定垂直于另一个平面.⑥用面面垂直的性质:两相交平面同时垂直于第三个平面,那么两平面的交线垂直于第三个平面.⑦利用向量证明.
与“如图,在直三棱柱ABC-A1B1C1中,侧面ABB1A1是边长为2的正方形...”考查相似的试题有:
- 在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点,(1)求证:EF∥平面ABC1D1;(2)求证:EF⊥B1C;(3)求三棱锥...
- 如图,四棱锥中,底面是菱形,,,是的中点,点在侧棱上.(1)求证:⊥平面;(2)若是的中点,求证://平面;(3)若,试求...
- 如图所示,PA⊥平面ABCD,ABCD是矩形,AB=1,,点F是PB的中点,点E在边BC上移动.(1)若,求证:;(2)若二面角的大小为,则CE为...
- 一个几何体的三视图如图所示:其中,主视图中大三角形的边长是2的正三角形,俯视图为正六边形,那么该几何体几的体积为 .
- 如图,三棱柱ABC—A1B1C1的侧棱AA1⊥底面ABC,∠ACB = 90°,E是棱CC1上中点,F是AB中点,AC = 1,BC = 2,AA1= 4.(1)求证:CF∥...
- 如图,已知圆锥体的侧面积为,底面半径和互相垂直,且,是母线的中点.(1)求圆锥体的体积;(2)异面直线与所成角的大小(结...
- 棱长为2的正方体的顶点都在同一球面上,则该球的表面积为 .
- 已知球O1,球O2,球O3的体积比为1∶8∶27,求它们的半径比.
- 三棱锥A-BCD中, E是BC的中点,AB=AD,BD⊥DC(I)求证:AE⊥BD;(II)若,且二面角A-BD-C为,求AD与面BCD所成角的正弦值。
- 如图,在长方体ABCD-A1B1C1D1中,已知AB=BC=1,BB1=。连接BC1,过B1作B1E⊥BC1交CC1于点E。(1)求证:AC1⊥平面B1D1E;(2)求...