本试题 “下列命题正确的是( )A.若=,则=B.若|+|=|-|,则=0C.若//,//,则//D.若与是单位向量,则=1” 主要考查您对向量共线的充要条件及坐标表示
向量数量积的运算
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 向量共线的充要条件及坐标表示
- 向量数量积的运算
向量共线的充要条件:
向量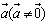 与
与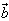 共线,当且仅当有唯一一个实数λ,使得
共线,当且仅当有唯一一个实数λ,使得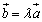 。
。
向量共线的几何表示:
设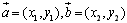 ,其中
,其中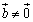 ,当且仅当
,当且仅当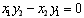 时,向量
时,向量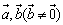 共线。
共线。
向量共线(平行)基本定理的理解:
(1)对于向量a(a≠0),b,如果有一个实数λ,使得b=λa,那么由向量数乘的定义知,a与b共线.
(2)反过来,已知向量a与b共线,a≠0,且向量b的长度是向量a的长度的μ倍,即|b|=μ|a|,那么当a与b同方向时,有b=μa;当a与b反方向时,有b=-μa.
(3)向量平行与直线平行是有区别的,直线平行不包括重合.
(4)判断a(a≠0)与b是否共线时,关键是寻找a前面的系数,如果系数有且只有一个,说明共线;如果找不到满足条件的系数,则这两个向量不共线.
(5)如果a=b=0,则数λ仍然存在,且此时λ并不唯一,是任意数值.
两个向量数量积的含义:
如果两个非零向量 ,
, ,它们的夹角为
,它们的夹角为 ,我们把数量
,我们把数量 叫做
叫做 与
与 的数量积(或内积或点积),记作:
的数量积(或内积或点积),记作: ,即
,即 。
。 叫
叫 在
在 上的投影。
上的投影。
规定:零向量与任一向量的数量积是0,注意数量积是一个实数,不再是一个向量。
数量积的的运算律:
已知向量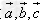 和实数λ,下面(1)(2)(3)分别叫做交换律,数乘结合律,分配律。
和实数λ,下面(1)(2)(3)分别叫做交换律,数乘结合律,分配律。
(1)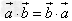 ;
;
(2)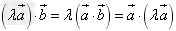 ;
;
(3)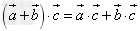 。
。
向量数量积的性质:
设两个非零向量
(1) ;
;
(2) ;
;
(3) ;
;
(4) ;
;
(5)当 ,
, 同向时,
同向时, ;当
;当 与
与 反向时,
反向时, ;当
;当 为锐角时,
为锐角时, 为正且
为正且 ,
, 不同向,
不同向, ;当
;当 为钝角时,
为钝角时, 为负且
为负且 ,
, 不反向,
不反向, 。
。
发现相似题
与“下列命题正确的是( )A.若=,则=B.若|+|=|-|,则=0C.若//,/...”考查相似的试题有:
- 已知点A(2,1),B(0,2),C(﹣2,1),O(0,0).给出下面的结论:①;②;③;④.其中正确结论的个数是( )个
- 过椭圆C:外一点A(m,0)作一直线l交椭圆于P、Q两点,又Q关于x轴对称点为Q1,连结PQ1交x轴于点B,(1)若,求证:;(2)求...
- 已知圆C:x2+(y-3)2=4,一动直线l过A(-1,0)与圆C相交于P,Q两点,M是PQ的中点,l与直线m:x+3y+6=0相交于N.(Ⅰ)当|PQ|...
- 如图,在△ABC中,AD⊥AB,,则=( )。
- 已知m=(cos,sin),n=(cos,sin),且满足|m+n|=。(1)求角A的大小;(2)若,试判断△ABC的形状。
- 异面直线l与m上的单位方向向量分别为a,b,且a•b=-12,则l与m的夹角的大小为______°.
- 若M为△ABC所在平面内一点,且满足则△ABC的形状为( ) A.正三角形 B.直角三角形 C.等腰三角形 D.等腰直角三角形
- 设点O是△ABC的三边中垂线的交点,且AC2-2AC+AB2=0,则BC•AO的范围是______.
- 若向量两两所成的角相等,且,则等于( ) A.2 B.5 C.2或5 D.或
- 设平面向量a=(cosx,sinx),b=(32,12),函数f(x)=a•b+1.①求函数f(x)的值域;②求函数f(x)的单调增区间.③当f(α)=95,且π...