本试题 “已知f(n)=1+123+133+143…+1n3,g(n)=32-12n2,n∈N*.(1)当n=1,2,3时,试比较f(n)与g(n)的大小关系;(2)猜想f(n)与g(n)的大小关系,并给出证明.” 主要考查您对不等式的定义及性质
数学归纳法证明不等式
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 不等式的定义及性质
- 数学归纳法证明不等式
不等式的定义:
一般地,用不等号表示不相等关系的式子叫做不等式,常见的不等号有“<”“>”“ ≤”“≥”及“≠”。
严格不等式的定义:
用“>"“<”连接的不等式叫做严格不等式。
非严格不等式的定义:
用“≤”和“≥”连接的不等式叫做非严格不等式.
特别提醒:a=b,a>b中,只要有一个成立,就有a≥b.
不等式的性质:
(1)如果a>b,那么b<a;如果b<a,那么a>b,即a>b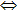 b<a;
b<a;
(2)如果a>b,b>c,那么a>c,即a>b,b>c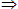 a>c;
a>c;
(3)如果a>b,那么a+c>b+c;
(4)如果a>b,c>0,那么ac>bc;如果a>b,c<0,那么ac<bc;
(5)如果a>b,c>d,那么a+c>b+d;
(6)如果a>b>0,c>d>0,那么ac>bd;
(7)如果a>b>0,那么an>bn(n∈N,n≥2);
(8)如果a>b>0,那么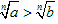 (n∈N,n≥2)。
(n∈N,n≥2)。
不等关系与不等式的区别:
不等关系强调的是量与量之间的关系,可以用符号“<…>…≤”“≥”来表示,也可以用语言表述;
而不等式则是用来表示不等关系的式子,可用“a>b”‘a<b”“a≥b a≤b”等式子来表示,不等关系是通过不等式来体现的.
不等式的分类:
①按成立的条件分:a.绝对不等式:不等式中的字母取任意实数值都恒成立的不等式叫做绝对不等式;b.条件不等式:不等式中的字母取某些允许值才能成立的不等式叫做条件不等式;c.矛盾不等式:不等式中的字母不论取何实数值都不能成立的不等式叫做矛盾不等式;
②按不等号开口方向分:a.同向不等式:不等号方向相同的两个不等式;b.异向不等式:不等号方向相反的两个不等式.
归纳法的定义:
由有限多个个别的特殊事例得出一般结论的推理方法,称为归纳法。
数学归纳法证明不等式的步骤:
(1)证明当n取初始值n0(例如n0=0,n0=1等)时不等式成立;
(2)假设当n=k(k为自然数,k≥n0)时不等式成立,证明当n=k+1时不等式也成立。
对数学归纳法的理解:
(1)数学归纳法是一种用于证明与自然数n有关的命题的正确性的证明方法.它的操作步骤简单、明确。
(2)运用数学归纳法证明与正整数有关的数学命题,两个步骤缺一不可.理解数学归纳法中的递推思想,尤其要注意其中第二步,证明n=k+1命题成立时必须要用到n=k时命题成立这个条件.这种理解不仅使我们能够正确认识数学归纳法的原理与本质,也为证明过程中第二步的设计指明了思维方向.
与“已知f(n)=1+123+133+143…+1n3,g(n)=32-12n2,n∈N*.(1)当n...”考查相似的试题有:
- 若a、b、c,则下列不等式成立的是( )A.B.C.D.
- (本小题满分12分)用分析法证明:;
- 已知1≤x≤3,-1≤y≤4,则3x+2y的取值范围是______.
- 若x
- 已知p:方程x2+mx+1=0有两个不等的负实根;q:对任意实数x不等式4x2+4(m-2)x+1>0恒成立,若p或q为真,p且q为假,求实数m的...
- 不等式的解集为 ;
- 某药店为了促销某种新药,计划在甲、乙两电视台做总时间不超过30分钟的广告,广告总费用不超过8000元,甲、乙电视台的收费标...
- 如果b<a<0那么下列不等式中的错误是( )A.a+b<abB.|a|>|b|C.1a<1b<0D.ba+ab>2
- 已知数列an满足递推关系式:2an+1=1-an2(n≥1,n∈N),且0<a1<1.(1)求a3的取值范围;(2)用数学归纳法证明:|an-(2-1)|...
- 设函数对任意实数x 、y都有,(1)求的值;(2)若,求、、的值;(3)在(2)的条件下,猜想的表达式,并用数学归纳法加以证...