本试题 “证明下面两个命题:(1)在所有周长相等的矩形中,只有正方形的面积最大;(2)余弦定理:如图,在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,则a2=b2+c2﹣2b...” 主要考查您对余弦定理
基本不等式及其应用
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 余弦定理
- 基本不等式及其应用
余弦定理:
三角形任意一边的平方等于其他两边的平方的和减去这两边与它们夹角的余弦的积的两倍,
即 。
。
推论:
在△ABC中,若a2+b2=c2,则C为直角;若a2+b2>c2,则C为锐角;若a2+b2<c2,则C为钝角。
余弦定理在解三角形中的应用:
(1)已知两边和夹角,
(2)已知三边。
其它公式:
射影公式: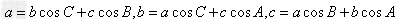
基本不等式:
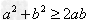 (当且仅当a=b时取“=”号);
(当且仅当a=b时取“=”号);
变式:①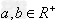 ,
,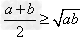 (当且仅当a=b时取“=”号),即两个正数的算术平均不小于它们的几何平均。
(当且仅当a=b时取“=”号),即两个正数的算术平均不小于它们的几何平均。
②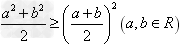 ;③
;③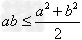 ;④
;④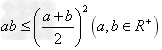 ;
;
对基本不等式的理解:
(1)基本不等式的证明是利用重要不等式推导的,即 ,即有
,即有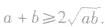
(2)基本不等式又称为均值定理、均值不等式等,其中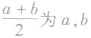 的算术平均数,
的算术平均数,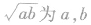 的几何平均数,本定理也可叙述为:两个正数的算术平均数不小于它们的几何平均数.
的几何平均数,本定理也可叙述为:两个正数的算术平均数不小于它们的几何平均数.
(3)要特别注意不等式成立的条件和等号成立的条件.均值不等式中:①当a=b时取等号,即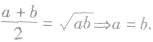
对于两个正数x,y,若已知xy,x+y,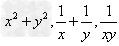 中的某一个为定值,可求出其余各个的最值:
中的某一个为定值,可求出其余各个的最值:
如:(1)当xy=P(定值),那么当x=y时,和x+y有最小值2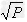 ,
,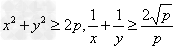 ;
;
(2)x+y=S(定值),那么当x=y时,积xy有最大值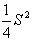 ,
,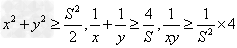 ;
;
(3)已知x2+y2=p,则x+y有最大值为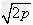 ,
, 。
。
应用基本的不等式解题时:
注意创设一个应用基本不等式的情境及使等号成立的条件,即“一正、二定、三相等”。
利用基本不等式比较实数大小:
(1)注意均值不等式的前提条件.
(2)通过加减项的方法配凑成使用均值定理的形式.
(3)注意“1”的代换.
(4)灵活变换基本不等式的形式,并注重其变形形式的运用.重要不等式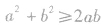 的形式可以是
的形式可以是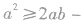
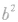 ,也可以是
,也可以是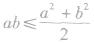 ,还可以是
,还可以是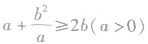 等,不仅要掌握原来的形式,还要掌握它的几种变形形式以及公式的逆用等,以便应用.
等,不仅要掌握原来的形式,还要掌握它的几种变形形式以及公式的逆用等,以便应用.
(5)合理配组,反复应用均值不等式。
基本不等式的几种变形公式:

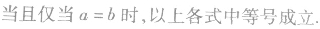
发现相似题
与“证明下面两个命题:(1)在所有周长相等的矩形中,只有正方形...”考查相似的试题有:
- 已知A、B、C为△ABC的三个内角,且其对边分别为a、b、c,且2cos2+cosA=0。(1)求角A的值;(2)若a=2,b+c=4,求△ABC的面积。
- 已知a,b,c分别为△ABC三个内角A,B,C的对边,b2+c2=a2+bc.(Ⅰ)求角A的大小;(Ⅱ)若b+c=23,a=2,求△ABC的面积.
- 在中,设内角的对边分别为,向量,向量,若(1)求角的大小;(2)若,且,求的面积.
- 设,则有( )A.B.C.D.
- 已知恒成立,则实数的取值范围是 .
- 若函数的值域为, 求实数的取值范围
- 已知x>0,y>0,且x+y=1,则1x+1y的最小值为( )A.1B.2C.3D.4
- (1)解不等式;(2)已知, 且, 求的最小值;
- 若a>0,b>0,且4a+b=1,则1a+4b的最小值是______.
- 已知两个正数x,y满足则xy最小值x,y值分别是 ( )A.5,5B.10,C.10,5D.10,10