本试题 “已知椭圆的离心率为，直线:与以原点为圆心、以椭圆的短半轴长为半径的圆相切.（1）求椭圆的方程；（2）设椭圆的左焦点为，右焦点，直线过点且垂直于椭圆的长...” 主要考查您对椭圆的定义
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 椭圆的定义
椭圆的第一定义：
平面内与两个定点为F1，F2的距离的和等于常数（大于
）的轨迹叫做椭圆，这两个定点叫做椭圆的焦点，两焦点的距离叫做椭圆的焦距。特别地，当常数等于时，轨迹是线段F1F2，当常数小于时，无轨迹。
椭圆的第二定义：
平面内到定点F的距离和到定直线l的距离之比等于常数e（0＜e＜1）的点的轨迹，叫做椭圆，定点F叫椭圆的焦点，定直线l叫做椭圆的准线，e叫椭圆的离心率。
椭圆的定义应该包含几个要素：
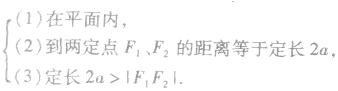
利用椭圆的定义解题：
当题目中出现一点在椭圆上的条件时，注意使用定义
发现相似题
与“已知椭圆的离心率为，直线:与以原点为圆心、以椭圆的短半轴长...”考查相似的试题有：
- 如下图，椭圆中心在坐标原点，焦点在坐标轴上，A、B是顶点，F是左焦点；当BF⊥AB时，此类椭圆称为 “黄金椭圆”，其离心率为。类...
- 在一椭圆中以焦点为直径两端点的圆，恰好过短轴的两顶点，则此椭圆的离心率等于 （ ）A．B．C．D．
- 以C：的焦点为顶点，顶点为焦点的椭圆的方程为
- 已知椭圆+=1,过点P(2，1)引一条弦，使它在这点被平分，求此弦所在的直线方程.
- 已知中顶点和顶点，顶点在椭圆上，则
- 已知△ABC的周长等于18，B、C两点坐标分别为（0，4），（0，-4），求A点的轨迹方程．
- 已知圆过椭圆的右顶点和右焦点，圆心在此椭圆上，那么圆心到椭圆中心的距离是 .
- 若直线和相交，则过点与椭圆的位置关系为( )A．点在椭圆内B．点在椭圆上C．点在椭圆外D．以上三种均有可能
- 已知椭圆的对称轴是坐标轴，离心率为，长轴长为，则椭圆方程为（ ）A．或B．C．或D．或
- 已知点P是椭圆上的动点，F1，F2分别为其左、右焦点，O是坐标原点，则的取值范围是 ．