本试题 “在平面直角坐标系xOy中，设曲线C1：所围成的封闭图形的面积为，曲线C1上的点到原点O的最短距离为．以曲线C1与坐标轴的交点为顶点的椭圆记为C2．（1）求椭圆C2...” 主要考查您对椭圆的定义
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 椭圆的定义
椭圆的第一定义：
平面内与两个定点为F1，F2的距离的和等于常数（大于
）的轨迹叫做椭圆，这两个定点叫做椭圆的焦点，两焦点的距离叫做椭圆的焦距。特别地，当常数等于时，轨迹是线段F1F2，当常数小于时，无轨迹。
椭圆的第二定义：
平面内到定点F的距离和到定直线l的距离之比等于常数e（0＜e＜1）的点的轨迹，叫做椭圆，定点F叫椭圆的焦点，定直线l叫做椭圆的准线，e叫椭圆的离心率。
椭圆的定义应该包含几个要素：
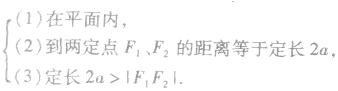
利用椭圆的定义解题：
当题目中出现一点在椭圆上的条件时，注意使用定义
发现相似题
与“在平面直角坐标系xOy中，设曲线C1：所围成的封闭图形的面积为...”考查相似的试题有：
- 根据下列条件求椭圆的标准方程：(1)两准线间的距离为，焦距为2；(2)已知P点在以坐标轴为对称轴的椭圆上，点P到两焦点的距离分...
- 若椭圆的离心率是，则的值为 .
- 设点P是椭圆上的一动点，F是椭圆的左焦点，则的取值范围为 ．
- (本小题满分13分) 设椭圆E中心在原点，焦点在x轴上，短轴长为4,点M（2，）在椭圆上，。（1）求椭圆E的方程；（2）设动直线L交...
- 点P(-3,1)在椭圆的左准线上，过点P斜率为的光线，经直线y=-2反射后通过椭圆的左焦点，则这个椭圆的离心率为A．B．C．D．
- （本小题满分13分）在平面直角坐标系中，已知椭圆：（）的左焦点为，且点在上.（Ⅰ）求椭圆的方程；（Ⅱ）已知直线的斜率为2且...
- 圆M与圆x2+y2=25内切，且经过点A（3，2），则圆心M在（ ）A．一个椭圆上B．双曲线的一支上C．一条抛物上D．一个圆上
- 已知椭圆两焦点F1、F2在y轴上，短轴长为2，离心率为，P是椭圆在第一象限弧上一点，且，过P作关于直线F1P对称的两条直线PA、PB...
- 椭圆中有如下结论：椭圆上斜率为1的弦的中点在直线上，类比上述结论：双曲线上斜率为1的弦的中点在直线 上
- 已知、为椭圆的焦点，且直线与椭圆相切．（Ⅰ）求椭圆方程；（Ⅱ）过的直线交椭圆于、两点，求△的面积的最大值，并求此时直线的...