本试题 “直线ρcosθ-ρsinθ=0的倾斜角是______.” 主要考查您对直线的方程
简单曲线的极坐标方程
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 直线的方程
- 简单曲线的极坐标方程
直线方程的定义:
以一个方程的解为坐标的点都是某条直线上的点,这个方程就叫做这条直线的方程,这条直线叫做这个方程的直线。
基本的思想和方法:
求直线方程是解析几何常见的问题之一,恰当选择方程的形式是每一步,然后釆用待定系数法确定方程,在求直线方程时,要注意斜率是否存在,利用截距式时,不能忽视截距为0的情形,同时要区分“截距”和“距离”。
直线方程的几种形式:
1.点斜式方程:
(1)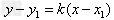 ,(直线l过点
,(直线l过点 ,且斜率为k)。
,且斜率为k)。
(2)当直线的斜率为0°时,k=0,直线的方程是y=y1。当直线的斜率为90°时,直线的斜率不存在,它的方程不能用点斜式表示,但因l上每一点的横坐标都等于x1,所以它的方程是x=x1。
2.斜截式方程:已知直线在y轴上的截距为b和斜率k,则直线的方程为:y=kx+b,它不包括垂直于x轴的直线。
3.两点式方程:已知直线经过(x1,y1),(x2,y2)两点,则直线方程为:
4.截距式方程:已知直线在x轴和y轴上的截距为a,b,则直线方程为: (a、b≠0)。
(a、b≠0)。
5.一般式方程:(1)定义:任何直线均可写成:Ax+By+C=0(A,B不同时为0)的形式。(2)特殊的方程如:平行于x轴的直线:y=b(b为常数);平行于y轴的直线:x=a(a为常数)。
几种特殊位置的直线方程:

(2)待定系数法:先设出直线的方程,再根据已知条件求出假设系数,最后代入直线方程,待定系数法常适用于斜截式,已知两点坐标等.
利用待定系数法求直线方程的步骤:①设方程;②求系数;③代入方程得直线方程,如果已知直线过一个定点
 ,可以利用直线的点斜式
,可以利用直线的点斜式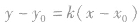 求方程,也可以利用斜截式、截距式等形式求解.
求方程,也可以利用斜截式、截距式等形式求解.曲线的极坐标方程的定义:
一般地,在极坐标系中,如果平面曲线C上任意一点的极坐标中至少有一个满足方程f(ρ,θ)=0,并且坐标适合方程f(ρ,θ)=0的点都在曲线上,那么方程f(ρ,θ)=0叫做曲线C的极坐标方程。
求曲线的极坐标方程的常用方法:
直译法、待定系数法、相关点法等。
圆心为(α,β)(a>0),半径为a的圆的极坐标方程为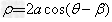 ,此圆过极点O。
,此圆过极点O。
直线的极坐标方程:
直线的极坐标方程是ρ=1/(2cosθ+4sinθ)。
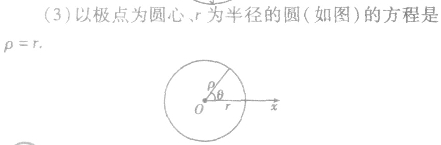
圆的极坐标方程:

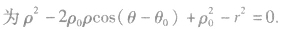

这是圆在极坐标系下的一般方程。


与“直线ρcosθ-ρsinθ=0的倾斜角是______.”考查相似的试题有:
- 过点(1,2)且与直线x+2y-1=0平行的直线方程是______.
- 已知直线:A1x+B1y+C1=0(C1≠0)与直线l2:A2x+B2y+C2=0(C2≠0)交于点M,O为坐标原点,则直线OM的方程为( )A.(A1C1-A2C2)...
- 直线x+2y+3=0的斜率和在y轴上的截距分别是 ( )A.和-3B.和-3C.和D.和
- 直线过点P(5,6),它在x轴上的截距是在y轴上的截距的2倍,则此直线方程为______.
- 已知A(1,2)、B(3,-4),则线段AB的垂直平分线的方程为______.
- 已知函数f(x)=x4-3x2+6,(Ⅰ)讨论f(x)的单调性;(Ⅱ)设点P在曲线y=f(x)上,若该曲线在点P处的切线l通过坐标原点,求l的方程.
- 求过点P(1,1),并且在两坐标轴上的截距相等的直线方程.
- 已知点A(5,2)、B(1,1)、C(1,)、P(x,y)在△ABC表示的区域内(包括边界)且目标函数z=ax+y(a>0)取得最大值的最优解有无穷多个,...
- 直线在轴和轴上的截距分别为和,直线的方程为,则直线到的角为A.30°B.45°C.135°D.45°或135°
- 过抛物线y2=4x的焦点F引两条互相垂直的直线AB、CD交抛物线于A、B、C、D四点.(1)求当|AB|+|CD|取最小值时直线AB、CD的倾斜...