本试题 “本题(1)、(2)、(3)三个选答题,每小题7分,请考生任选2题作答,满分14分,如果多做,则按所做的前两题计分.作答时,先用2B铅笔在答题卡上把所选题目对...” 主要考查您对绝对值不等式
简单曲线的极坐标方程
直线的参数方程
矩阵与变换
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 绝对值不等式
- 简单曲线的极坐标方程
- 直线的参数方程
- 矩阵与变换
绝对值不等式:
当a>0时,有 ;
;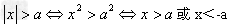 或x<-a 。
或x<-a 。
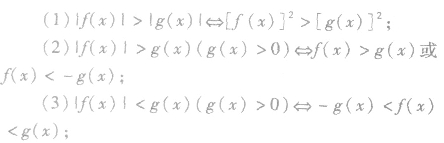
(4)含两个或两个以上绝对值符号的不等式可用零点分区间的方法去绝对值符号求解,也可以用图象法求解。
曲线的极坐标方程的定义:
一般地,在极坐标系中,如果平面曲线C上任意一点的极坐标中至少有一个满足方程f(ρ,θ)=0,并且坐标适合方程f(ρ,θ)=0的点都在曲线上,那么方程f(ρ,θ)=0叫做曲线C的极坐标方程。
求曲线的极坐标方程的常用方法:
直译法、待定系数法、相关点法等。
圆心为(α,β)(a>0),半径为a的圆的极坐标方程为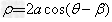 ,此圆过极点O。
,此圆过极点O。
直线的极坐标方程:
直线的极坐标方程是ρ=1/(2cosθ+4sinθ)。
圆的极坐标方程:

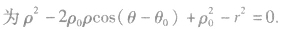

这是圆在极坐标系下的一般方程。


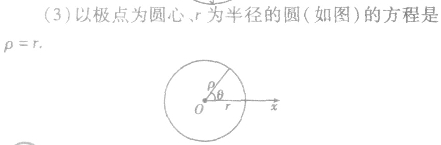
直线的参数方程:
过定点 倾斜角为α的直线的参数方程为
倾斜角为α的直线的参数方程为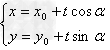 (t为参数)。
(t为参数)。
直线的参数方程及其推导过程:
设e是与直线l平行且方向向上(l的倾斜角不为0)或向右(l的倾斜角为0)的单位方向向量(单位长度与坐标轴的单位长度相同).直线l的倾斜角为α,定点M0、动点M的坐标分别为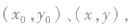
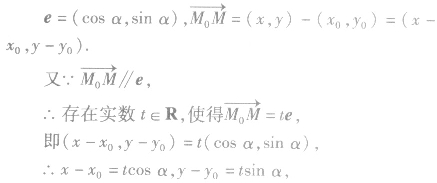

直线的参数方程中参数t的几何意义是: 表示参数t对应的点M到定点Mo的距离,当
表示参数t对应的点M到定点Mo的距离,当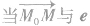 同向时,t取正数;当
同向时,t取正数;当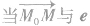 异向时,t取负数;当点M与Mo重合时,t=0.
异向时,t取负数;当点M与Mo重合时,t=0.
矩阵的定义:
由m×n个数排成的m行n列的表
称为m行n列矩阵(matrix),简称m×n矩阵。
特殊形式矩阵:
(1)n阶方阵:在矩阵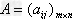 中,当m=n时,A称为n阶方阵;
中,当m=n时,A称为n阶方阵;
(2)行矩阵:只有一行的矩阵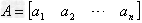 叫做行矩阵;
叫做行矩阵;
列矩阵:只有一列的矩阵,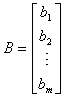 叫做列矩阵;
叫做列矩阵;
(3)零矩阵:元素都是零的矩阵称作零矩阵。
二阶矩阵与平面图形的变换:
(1)二阶矩阵的定义:由4个数a,b,c,d排成的正方形数表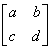 称为二阶矩阵;
称为二阶矩阵;
(2)几种特殊线性变换:主要有旋转变换、反射变换、伸压变换、投影变换、切变变换这几种。求经矩阵变换后的解析式常采用数形结合的方法,先观察是属于哪一种变换,然后利用解析几何中的相关点法(转移代入法)来解。
矩阵的运算律:
(1)矩阵的和(差):当两个矩阵A、B的维数相同时,将它们各位置上的元素加(减)所得到的矩阵称为矩阵A、B的和(差),记作: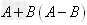 。
。
运算律:加法运算律: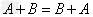 ;
;
加法结合律: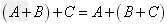 。
。
(2)数乘矩阵:矩阵与实数的积:设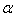 为任意实数,把矩阵A的所有元素与
为任意实数,把矩阵A的所有元素与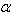 相乘得到的矩阵叫做矩阵A与实数
相乘得到的矩阵叫做矩阵A与实数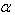 的乘积矩阵,记作:
的乘积矩阵,记作: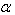 A。
A。
运算律:(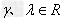 )
)
分配律: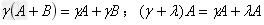 ;
;
结合律: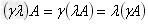 。
。
(3)矩阵的乘积:一般地,设A是m×k阶矩阵,B是k×n阶矩阵,设C为m×n矩阵,如果矩阵C中第i行第j列元素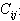 是矩阵A第i个行向量与矩阵B的第j个列向量的数量积,那么矩阵C叫做A与B的乘积,记作:C=AB。
是矩阵A第i个行向量与矩阵B的第j个列向量的数量积,那么矩阵C叫做A与B的乘积,记作:C=AB。
运算律:
分配律: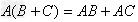 ;
;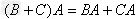 ;
;
结合律: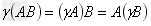 ;
;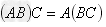 。
。
注:(1)交换律不成立,即:AB≠BA;(2)只有当矩阵A的列数与矩阵B的行数相等时,矩阵之积才有意义。
与“本题(1)、(2)、(3)三个选答题,每小题7分,请考生任选2...”考查相似的试题有:
- 函数y=|x-1|+|x-3|的最小值是______.
- 若f(x)是R上的减函数,且f(x)的图象过点(0,3)和(3,-1),则不等式|f(x+1)-1|<2的解集( )A.(-∞,2)B.(-1,...
- 若,则的最小值是 .
- 选修4-5:不等式选讲设函数f(x)=|x-1|+|2x-3|-a.(I)当a=2时,求不等式f(x)≥0的解集;(II )若f(x)≥O恒成立,求a的...
- 在极坐标中,圆ρ=2cosθ的圆心的极坐标是( ),它与方程θ=(ρ>0)所表示的图形的交点的极坐标是( )。
- 在极坐标系中,直线θ=π6(ρ∈R)截圆ρ=2cos(θ-π6)所得弦长是______.
- 已知直线l的参数方程为(t为参数),曲线C的极坐标方程为,以极点为原点,极轴为x轴正半轴建立直角坐标系,M点坐标为(0,2)...
- 直线x=1+ty=1-t(t为参数)的倾斜角的大小为( )A.-π4B.π4C.π2D.3π4
- 在平面直角坐标系xOy中,直线l:x+y+2=0在矩阵M=对应的变换作用下得到直线m:x-y-4=0,求实数a、b的值.
- [选修4-2:矩阵与变换]已知矩阵,向量,是实数,若,求的值.