本试题 “求与x-2y=0平行,且过直线4x+3y-10=0和2x-y-10=0的交点的直线方程.” 主要考查您对异面直线所成的角
直线的方程
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 异面直线所成的角
- 直线的方程
异面直线所成角的定义:
直线a、b是异面直线,经过空间任意一点O,分别引直线a′∥a,b′∥b,则把直线a′和b′所成的锐角(或直角)叫做异面直线a和b所成的角,如下图。
两条异面直线所成角的范围是(0°,90°],若两条异面直线所成的角是直角,我们就说这两条异面直线互相垂直。
在异面直线所成角定义中,空间一点O是任取的,而和点O的位置无关。 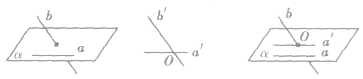
求异面直线所成角的步骤:
A、利用定义构造角,可固定一条,平移另一条,或两条同时平移到某个特殊的位置,顶点选在特殊的位置上。
B、证明作出的角即为所求角;
C、利用三角形来求角。
特别提醒:
(1)两异面直线所成的角与点O(两直线平移后的交点)的选取无关.
(2)两异面直线所成角θ的取值范围是00<θ≤900.
(3)判定空间两条直线是异面直线的方法①判定定理:平面外一点A与平面内一点B的连线和平面内不过点B的直线是异面直线;②反证法:证明两直线共面不可能.
线线角的求法:
(1)定义法:用“平移转化”,使之成为两相交直线所成的角,当异面直线垂直时,应用线面垂直定义或三垂线定理及逆定理判定所成的角为900.
(2)向量法:设两条直线所成的角为θ(锐角),直线l1和l2的方向向量分别为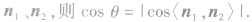
直线方程的定义:
以一个方程的解为坐标的点都是某条直线上的点,这个方程就叫做这条直线的方程,这条直线叫做这个方程的直线。
基本的思想和方法:
求直线方程是解析几何常见的问题之一,恰当选择方程的形式是每一步,然后釆用待定系数法确定方程,在求直线方程时,要注意斜率是否存在,利用截距式时,不能忽视截距为0的情形,同时要区分“截距”和“距离”。
直线方程的几种形式:
1.点斜式方程:
(1)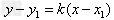 ,(直线l过点
,(直线l过点 ,且斜率为k)。
,且斜率为k)。
(2)当直线的斜率为0°时,k=0,直线的方程是y=y1。当直线的斜率为90°时,直线的斜率不存在,它的方程不能用点斜式表示,但因l上每一点的横坐标都等于x1,所以它的方程是x=x1。
2.斜截式方程:已知直线在y轴上的截距为b和斜率k,则直线的方程为:y=kx+b,它不包括垂直于x轴的直线。
3.两点式方程:已知直线经过(x1,y1),(x2,y2)两点,则直线方程为:
4.截距式方程:已知直线在x轴和y轴上的截距为a,b,则直线方程为: (a、b≠0)。
(a、b≠0)。
5.一般式方程:(1)定义:任何直线均可写成:Ax+By+C=0(A,B不同时为0)的形式。(2)特殊的方程如:平行于x轴的直线:y=b(b为常数);平行于y轴的直线:x=a(a为常数)。
几种特殊位置的直线方程:

(2)待定系数法:先设出直线的方程,再根据已知条件求出假设系数,最后代入直线方程,待定系数法常适用于斜截式,已知两点坐标等.
利用待定系数法求直线方程的步骤:①设方程;②求系数;③代入方程得直线方程,如果已知直线过一个定点
 ,可以利用直线的点斜式
,可以利用直线的点斜式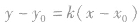 求方程,也可以利用斜截式、截距式等形式求解.
求方程,也可以利用斜截式、截距式等形式求解.与“求与x-2y=0平行,且过直线4x+3y-10=0和2x-y-10=0的交点的直线...”考查相似的试题有:
- 如图,正三棱锥SABC的侧棱与底面边长相等,如果E、F分别为SC、AB的中点,那么异面直线EF与SA所成的角等于( )A.90°B.60°C...
- 如图1,已知点P在矩形ABCD边DC上,AB=2,BC=1,点F在AB上且DF⊥AP,垂足为E,将△ADP沿AP折起,使点D位于点D'位置,连接D'B,D'...
- 设A,B,C,D是不共面的四个点,P,Q,S,R为AC,BC,DB,DA的中点,若AB=,CD=,且四边形PQRS的面积为,则异面直线AB与CD所...
- 如图,已知四棱锥P-ABCD的底面ABCD为等腰梯形,AB∥CD,AC⊥DB,AC与BD相交于点O,且顶点P在底面上的射影恰为O点,又BO=2,PO=...
- 已知两直线a1x+b1y+1=0与a2x+b2y+1=0的交点为P(2,3),则过点Q1(a1,b1),Q2(a2,b2)的直线方程为( )
- 过点且在两坐标轴上截距相等的直线的方程为
- 直线过原点且平分的面积,若平行四边形的两个顶点为,则直线的方程为________________。
- 直线l1:2x-y+1=0与l2:4x-2y+3=0的位置关系.
- 已知的顶点、、,边上的中线所在直线为.(1)求的方程;(2)求点A关于直线的对称点的坐标。
- 过点且与直线平行的直线方程是( )A.B.C.D.