本试题 “设O、A、B、C为平面内四点,OA=a,OB=b,OC=c,且a+b+c=0,a•b=b•c=c•a=-1,则|a|2+|b|2+|c|2=______.” 主要考查您对向量模的计算
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 向量模的计算
向量的模:
设 ,则有向线段
,则有向线段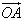 的长度叫做向量
的长度叫做向量 的长度或模,记作:
的长度或模,记作: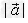 ,则
,则  。
。
向量模的坐标表示:
(1)若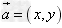 ,则
,则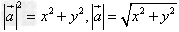 ;
;
(2)若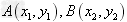 ,那么
,那么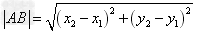 。
。
求向量的模:
求向量的模主要是利用公式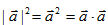 来解。
来解。
发现相似题
与“设O、A、B、C为平面内四点,OA=a,OB=b,OC=c,且a+b+c=0,a•...”考查相似的试题有:
- 在平面直角坐标系中,O为坐标原点,点A(-1,-2)、B(2,3)、C(-2,-1)。(1)求以线段AB、AC为邻边的平行四边形两条对角...
- 已知向量a,b满足|a|=1,|b|=2,|a-b|=2,则|a+b|=______.
- 下列各式中错误的是( ) A.||2=2 B.||=|| C.0•=0 D.m(n)=mn(m,n∈R)
- 已知向量夹角为45°,且=4,,则=( )。
- 已知a,b是两个单位向量,向量p=a+b,则|p|的取值范围是______.
- 已知a=(-1,2),b=(λ,1),若|2a-b|=5,则λ=______.
- 已知:A(cosx,sinx),B(1,1),+=,f(x)=.(Ⅰ)求f(x)的对称轴和对称中心;(Ⅱ)求f(x)的单调递增区间.
- 已知单位向量a,b,其夹角为π3,则|a+b|=( )A.3B.3C.2D.2
- 若向量、满足,,且与的夹角为,则=( )
- 设单位向量e1,e2满足e1•e2=-12,|e1+2e2|=则______.