设二次函数f(x)=x2+bx+c(b,c∈R),已知不论α、β为何实数恒有f(sinα)≥0和f(2+cosβ)≤0。(1)求证:b+c=,高中三年级,数学试题,任意角的三角函数考点,好技网

解答题

设二次函数f(x)=x²+bx+c(b,c∈R),已知不论α、β为何实数恒有f(sinα)≥0和f(2+cosβ)≤0。
(1)求证: b+c=－1；
(2)求证c≥3；
(3)若函数f(sinα)的最大值为8，求b，c的值.

本题信息：数学解答题难度一般来源:未知
本题答案
查看答案

本试题 “设二次函数f(x)=x2+bx+c(b,c∈R),已知不论α、β为何实数恒有f(sinα)≥0和f(2+cosβ)≤0。(1)求证:b+c=－1；(2)求证c≥3；(3)若函数f(sinα)的最大值为8，求b，c的值.” 主要考查您对
任意角的三角函数
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。

任意角的三角函数

任意角的三角函数的定义：

设α是任意一个角，α的终边上任意一点P的坐标是（x，y），它与原点的距离是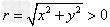，那么，，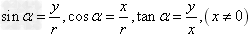
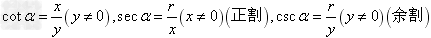以上以角为自变量，比值为函数的六个函数统称为三角函数。三角函数值只与角的大小有关，而与终边上点P的位置无关。

象限角的三角函数符号：

一全正，二正弦，三两切，四余弦。

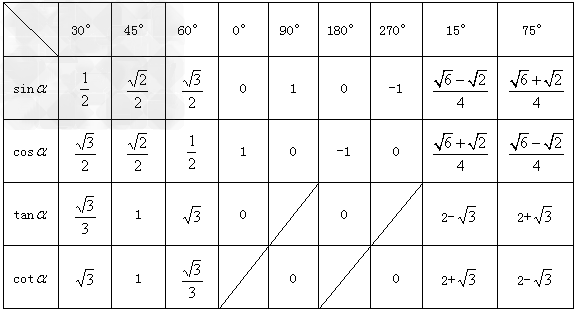
特殊角的三角函数值：（见下表）

发现相似题

与“设二次函数f(x)=x2+bx+c(b,c∈R),已知不论α、β为何实数恒有f(s...”考查相似的试题有：