返回

高中一年级数学

首页
首页 高中一年级数学知识 正弦、余弦函数的图象与性质（定义域、值域、单调性、奇偶性等） 正切、余切函数的图象与性质（定义域、值域、单调性、奇偶性等） 试题正文
  • 解答题
    在中，内角所对边长分别为，，．
    (1)求的最大值及的取值范围；
    (2)求函数的值域．

    本题信息：数学解答题难度一般 来源:未知
  • 本题答案
    查看答案
本试题 “在中，内角所对边长分别为，，．(1)求的最大值及的取值范围；(2)求函数的值域．” 主要考查您对

正弦、余弦函数的图象与性质（定义域、值域、单调性、奇偶性等）

正切、余切函数的图象与性质（定义域、值域、单调性、奇偶性等）

等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
  • 正弦、余弦函数的图象与性质（定义域、值域、单调性、奇偶性等）
  • 正切、余切函数的图象与性质（定义域、值域、单调性、奇偶性等）

正弦函数和余弦函数的图象：正弦函数y=sinx（x∈R）和余弦函数y=cosx（x∈R）的图象分别叫做正弦曲线和余弦曲线，

1．正弦函数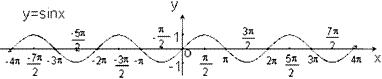

2．余弦函数

函数图像的性质
正弦、余弦函数图象的性质：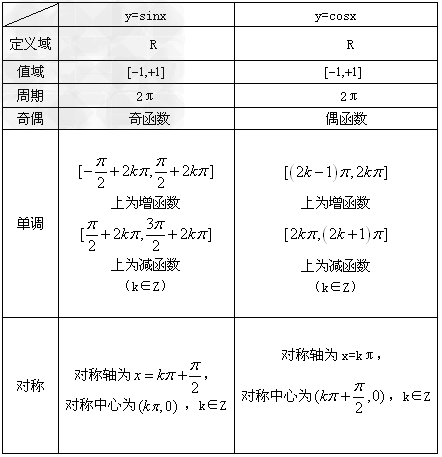

由上表知，正弦与余弦函数的定义域都是R，值域都是[-1，1]，对y=sinx，当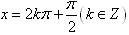时，y取最大值1，
当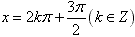时，y取最小值-1；对y=cosx，当x=2kπ（k∈Z）时，y取最大值1，当x=2kπ+π（k∈Z）时，y取最小值-1。




正弦、余弦函数图象的性质：


由上表知，正弦与余弦函数的定义域都是R，值域都是[-1，1]，对y=sinx，当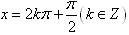时，y取最大值1，
当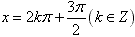时，y取最小值-1；对y=cosx，当x=2kπ（k∈Z）时，y取最大值1，当x=2kπ+π（k∈Z）时，y取最小值-1。


正切函数的图像：

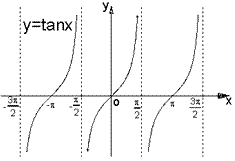
余切函数的图像：



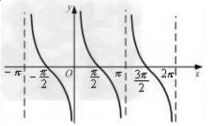
正切函数的性质：

（1）定义域：；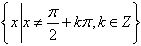
（2）值域是R，在上面定义域上无最大值也无最小值；
（3）周期性：是周期函数且周期是π，它与直线y=a的两个相邻交点之间的距离是一个周期π；
（4）奇偶性：是奇函数，对称中心是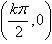（k∈Z），无对称轴；
（5）单调性：正切函数在开区间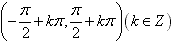内都是增函数。但要注意在整个定义域上不具有单调性。

余切函数的性质:

（1）定义域：{x|x≠kπ，k∈Z}
（2）值域：实数集R；
（3）周期性：是周期函数，周期为kπ（k∈Z且k≠0），最小正周期T=π
（4）奇偶性：奇函数，图像关于（，0）（k∈z）对称，实际上所有的零点都是它的对称中心
（5）单调性：在每一个开区间（kπ，（k+1）π），（k∈Z）上都是减函数，在整个定义域上不具有单调性 

 


发现相似题
与“在中，内角所对边长分别为，，．(1)求的最大值及的取值范围；...”考查相似的试题有：