本试题 “(1)函数f(x)=ax(a>0,且a≠1)在区间[1,2]上的最大值比最小值大,求a的值;(2)如果函数y=a2x+2ax-1(a>0,且a≠1)在[ -1,1]上有最大值14,试求a的值。” 主要考查您对二次函数的性质及应用
指数函数的图象与性质
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 二次函数的性质及应用
- 指数函数的图象与性质
二次函数的定义:
一般地,如果 (a,b,c是常数,a≠0),那么y叫做x的二次函数。
(a,b,c是常数,a≠0),那么y叫做x的二次函数。
二次函数的图像:
是一条关于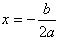 对称的曲线,这条曲线叫抛物线。
对称的曲线,这条曲线叫抛物线。
抛物线的主要特征:①有开口方向,a表示开口方向;a>0时,抛物线开口向上;a<0时,抛物线开口向下;
②有对称轴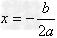 ;
;
③有顶点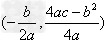 ;
;
④c表示抛物线与y轴的交点坐标:(0,c)。
性质:二次函数y=ax2+bx+c,
①当a>0时,函数f(x)的图象开口向上,在(-∞,-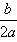 )上是减函数,在[-
)上是减函数,在[- ,+∞)上是增函数;
,+∞)上是增函数;
②当a<0时,函数f(x)的图象开口向下,在(-∞,-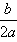 )上是增函数,在[-
)上是增函数,在[-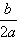 ,+∞)是减函数。
,+∞)是减函数。
二次函数 (a,b,c是常数,a≠0)的图像:
(a,b,c是常数,a≠0)的图像:
| 图像 | 函数的性质 | ||
| a>0 | 定义域 | x∈R(个别题目有限制的,由解析式确定) | |
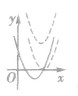 |
值域 | a>0 | a<0 |
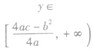 |
 | ||
| 奇偶性 | b=0时为偶函数,b≠0时为非奇非偶函数 | ||
| a<0 | 单调性 | a>0 | a<0 |
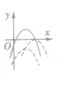 |
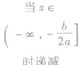 |
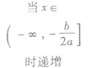 | |
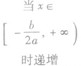 |
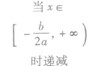 | ||
| 图像特点 |
 | ||
二次函数的解析式:
(1)一般式: (a,b,c是常数,a≠0);
(a,b,c是常数,a≠0);
(2)顶点式:若二次函数的顶点坐标为(h,k),则其解析式为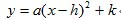 ;
;
(3)双根式:若相应一元二次方程的两个根为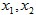 ,则其解析式为
,则其解析式为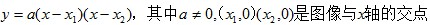 。
。
二次函数在闭区间上的最值的求法:
(1)二次函数![]() 在区间[p,g]上的最值问题
在区间[p,g]上的最值问题
一般情况下,需要分![]()
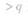 三种情况讨论解决.
三种情况讨论解决.
当a>0时,f(x)在区间[p,g]上的最大值为M,最小值为m,令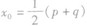 .
.
①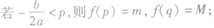
②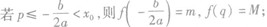
③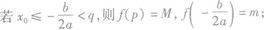
④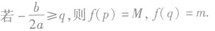
特别提醒:在区间内同时讨论最大值和最小值需要分四种情况讨论.
(2)二次函数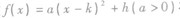 在区间[m.n]上的最值问题一般地,有以下结论:
在区间[m.n]上的最值问题一般地,有以下结论:
特别提醒:max{1,2}=2,即取集合{1,2}中最大的元素。
二次函数的应用:
(1)应用二次函数才解决实际问题的一般思路:
理解题意;建立数学模型;解决题目提出的问题。
(2)应用二次函数求实际问题中的最值:
即解二次函数最值应用题,设法把关于最值的实际问题转化为二次函数的最值问题,然后按求二次函数最值的方法求解。求最值时,要注意求得答案要符合实际问题。
指数函数y=ax(a>0,且a≠1)的图象和性质:
| 0<a<1 | a>1 | ||
| 图像 | 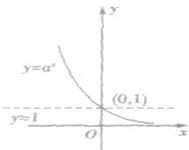 |
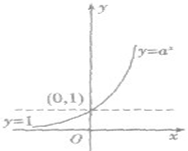 | |
| 图像 | 定义域 | R | |
| 值域 | (0,+∞) | ||
| 恒过定点 | 图像恒过定点(0,1),即当x等于0时,y=1 | ||
| 单调性 | 在(-∞,+∞)上是减函数 | 在(-∞,+∞)上是增函数 | |
| 函数值的变化规律 | 当x<0时,y>1 | 当x<0时,0<y<1 | |
| 当x=0时,y=1 | 当x=0时,y=1 | ||
| 当x>0时,0<y<1 | 当x>0时,y>1 | ||
底数对指数函数的影响:
①在同一坐标系内分别作函数的图象,易看出:当a>l时,底数越大,函数图象在第一象限越靠近y轴;同样地,当0<a<l时,底数越小,函数图象在第一象限越靠近x轴.
②底数对函数值的影响如图.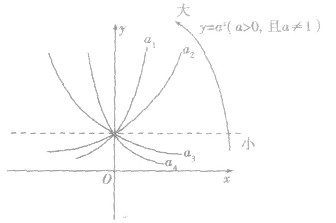
③当a>0,且a≠l时,函数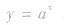 与函数y=
与函数y=![]() 的图象关于y轴对称。
的图象关于y轴对称。
利用指数函数的性质比较大小:
若底数相同而指数不同,用指数函数的单调性比较:
若底数不同而指数相同,用作商法比较;
若底数、指数均不同,借助中间量,同时要注意结合图象及特殊值,
指数函数图象的应用:
函数的图象是直观地表示函数的一种方法.函数的很多性质,可以从图象上一览无余.数形结合就是几何与代数方法紧密结合的一种数学思想.指数函数的图象通过平移、翻转等变可得出一般函数的图象.利用指数函数的图象,可解决与指数函数有关的比较大小、研究单调性、方程解的个数、求值域或最值等问题.
与“(1)函数f(x)=ax(a>0,且a≠1)在区间[1,2]上的最大值比...”考查相似的试题有:
- 在R上是增函数,则有A.B.C.D.
- 若函数f(x)=x2+2a|x|+4a2﹣1的零点有且只有一个,则实数a=( ).
- 关于x的一元二次不等式ax2-ax+1>0对于一切实数x都成立的充要条件______.
- 已知f(x)=(x–a)(x–b)–2(其中a<b,且α、β是方程f(x)=0的两根(α<β,则实数a、b、α、β的大小关系为( )A.α<a<b<βB.α<a...
- 函数y=-x2+2|x|,单调递减区间为______.
- x0是x的方程ax=logax(0<a<1)的解,则x0,1,a这三个数的大小关系是______.
- 在下列图像中,二次函数y=ax2+bx及指数函数的图像只可能是[ ]A、B、C、D、
- 在平面直角坐标系中,横纵坐标均为整数的点称为格点,如果函数f(x)的图象恰好通过k(k∈N*)个格点,则称函数f(x)为k阶格...
- 函数y=2的图象与直线y=x的位置关系是( ) A. B. C. D.
- 函数y=ax+b(0<a<1)的图象与x负半轴相交于一点,则b的取值范围为______.