本试题 “(本小题满分15分)如图所示,一科学考察船从港口出发,沿北偏东角的射线方向航行,而在离港口(为正常数)海里的北偏东角的A处有一个供给科考船物资的小岛,...” 主要考查您对正弦定理
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 正弦定理
正弦定理:
在一个三角形中,各边和它所对角的正弦的比相等,即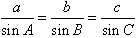 =2R。
=2R。
有以下一些变式:
(1)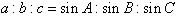 ;
;
(2)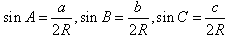 ;
;
(3)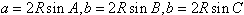 。
。
正弦定理在解三角形中的应用:
(1)已知两角和一边解三角形,只有一解。
(2)已知两边和其中一边的对角,解三角形,要注意对解的个数的讨论。可按如下步骤和方法进行:先看已知角的性质和已知两边的大小关系。
如已知a,b,A,
(一)若A为钝角或直角,当b≥a时,则无解;当a≥b时,有只有一个解;
(二)若A为锐角,结合下图理解。
①若a≥b或a=bsinA,则只有一个解。
②若bsinA<a<b,则有两解。
③若a<bsinA,则无解。 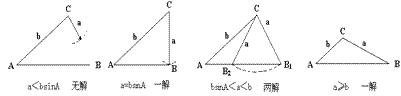
也可根据a,b的关系及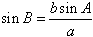 与1的大小关系来确定。
与1的大小关系来确定。
发现相似题
与“(本小题满分15分)如图所示,一科学考察船从港口出发,沿北...”考查相似的试题有:
- 在△ABC中,BD为∠ABC的平分线,AB = 3,BC = 2,AC = ,则=A.B.C.D.
- 在中,,,则( )A.B.C.D.
- 已知△ABC中,A、B、C分别为三个内角,a、b、c为所对边,22(sin2A-sin2C)=(a-b)sinB,△ABC的外接圆半径为2,(1)求角C;...
- 在△ABC中,下列关系式不一定成立的是[ ]A.asinB=bsinAB.a=bcosC+ccosBC.a+b-c=2abcosCD.b=csinA+asinC
- 在△ABC中,角A,B,C的对边分别为a,b,c,cosA=34,C=2A.(Ⅰ)求cosC的值;(Ⅱ)若ac=24,求a,c的值.
- 已知下列命题:①;②函数y=f(|x|﹣1)的图象向左平移1个单位后得到的函数图象解析式为y=f(|x|);③函数y=f(1+x)的图象与函...
- 在△中,内角、、的对边分别为、、,已知,,,则 .
- 已知△ABC中,AB=AC,则cosB+cosA的最大值为______.
- 如图, 在中,,是边上一点,,则的长为 .
- 已知是的内角,并且有,则______。