返回

高中二年级数学

首页
首页 高中二年级数学知识 点到直线的距离 直线与抛物线的应用 试题正文
  • 解答题
    已知A、B 是抛物线y2=4x上的两点，O是抛物线的顶点，OA⊥OB ．
    (1) 求证：直线AB 过定点M(4，0) ；
    (2) 设弦AB 的中点为P，求点P 到直线x-y=0的距离的最小值．
    本题信息：2012年期末题数学解答题难度较难 来源:刘建昰
  • 本题答案
    查看答案
本试题 “已知A、B 是抛物线y2=4x上的两点，O是抛物线的顶点，OA⊥OB ．(1) 求证：直线AB 过定点M(4，0) ；(2) 设弦AB 的中点为P，求点P 到直线x-y=0的距离的最小值．” 主要考查您对

点到直线的距离

直线与抛物线的应用

等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
  • 点到直线的距离
  • 直线与抛物线的应用

点到直线的距离公式：

1、若点P（x0，y0）在直线Ax+By+C=0（A，B不同时为0）上，则Ax0+By0+C=0。
2、若点P（x0，y0）不在直线Ax+By+C=0（A，B不同时为0）上，则Ax0+By0+C≠0，此时点P（x0，y0）直线Ax+By+C=0（A，B不同时为0）的距离d=。


点到直线的距离公式的理解：

①点到直线的距离是直线上的点与直线外一点的连线的最短距离（这是从运动观点来看的）．
②若给出的直线方程不是一般式，则应先把方程化为一般式，再利用公式求距离．
③点到直线的距离公式适用于任何情况，其中点P在直线l上时，它到直线的距离为0．
④点到几种特殊直线的距离：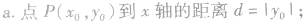
 

 

 
 

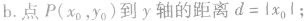
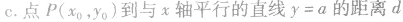
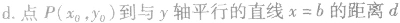
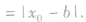
设直线l的方程为：Ax+By+C=0（A、B不同时为零），抛物线的方程为y2=2px（p＞0），将直线的方程代入抛物线的方程，消去y（或x） 得到一元二次方程，进而应用根与系数的关系解题。

直线与抛物线的位置关系:

直线和抛物线的位置关系，可通过直线方程与抛物线方程组成的方程组的实数解的个数来确定，同时注意过焦点的弦的一些性质，如：


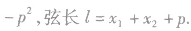
发现相似题
与“已知A、B 是抛物线y2=4x上的两点，O是抛物线的顶点，OA⊥OB ．...”考查相似的试题有：