本试题 “设AB为过抛物线y2=2px(p>0)的焦点的弦,则|AB|的最小值为( ) A. B.P C.2P D.无法确定” 主要考查您对直线与抛物线的应用
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 直线与抛物线的应用
设直线l的方程为:Ax+By+C=0(A、B不同时为零),抛物线的方程为y2=2px(p>0),将直线的方程代入抛物线的方程,消去y(或x) 得到一元二次方程,进而应用根与系数的关系解题。
直线与抛物线的位置关系:
直线和抛物线的位置关系,可通过直线方程与抛物线方程组成的方程组的实数解的个数来确定,同时注意过焦点的弦的一些性质,如:
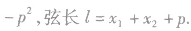
发现相似题
与“设AB为过抛物线y2=2px(p>0)的焦点的弦,则|AB|的最小值为...”考查相似的试题有:
- 在平面直角坐标系xOy中,点P到点F(3,0)的距离的4倍与它到直线x=2的距离的3倍之和记为d,当P点运动时,d恒等于点P的横坐标...
- 正方形的一条边AB在直线y=x+4上,顶点C、D在抛物线上,求正方形的边长。
- 设抛物线y2=x的焦点为F,点M在抛物线上,线段MF的延长线与直线交于点N,则的值为[ ]A.B.C.2D.4
- 已知抛物线C:y2=2px(p>0)的准线为l,过M(1,0)且斜率为的直线与l相交于点A,与C的一个交点为B.若,则p=( )。
- 过抛物线y2=4x的焦点作直线与其交于M、N两点,作平行四边形MONP,则P点的轨迹方程为( ) A.y2=4(x-2) B.y2=-4(x+2) C...
- 设抛物线x2=12y的焦点为F,经过点P(2,1)的直线l与抛物线相交于A、B两点,又知点P恰为AB的中点,则|AF|+|BF|=( )。
- 学习了圆锥曲线及其方程后,对于一个一般的二元二次方程:Ax2+Cy2+Dx+Ey+F=0(A,C,D,E,F为常数),请你写出一个它分别表...
- 抛物线的顶点在原点,焦点在射线x﹣y+1=0(x≥0)上(1)求抛物线的标准方程(2)过(1)中抛物线的焦点F作动弦AB,过A、B两点...
- 某抛物线形拱桥的跨度为20米,拱高是4米,在建桥时,每隔4米需用一根柱支撑,其中最高支柱的高度是______.
- 设抛物线y2=2px(p>0)的焦点为F,经过点F的直线交抛物线于A、B两点,点C在抛物线的准线上,且BC∥x轴, 证明直线AC经过原点O。