本试题 “下列判断正确的是[ ]A.1.72.5>1.73B.0.82<0.83C.D.1.70.3>0.90.3” 主要考查您对指数函数的图象与性质
幂函数
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 指数函数的图象与性质
- 幂函数
指数函数y=ax(a>0,且a≠1)的图象和性质:
| 0<a<1 | a>1 | ||
| 图像 | 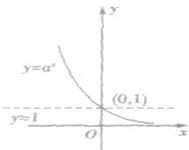 |
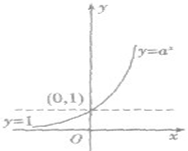 | |
| 图像 | 定义域 | R | |
| 值域 | (0,+∞) | ||
| 恒过定点 | 图像恒过定点(0,1),即当x等于0时,y=1 | ||
| 单调性 | 在(-∞,+∞)上是减函数 | 在(-∞,+∞)上是增函数 | |
| 函数值的变化规律 | 当x<0时,y>1 | 当x<0时,0<y<1 | |
| 当x=0时,y=1 | 当x=0时,y=1 | ||
| 当x>0时,0<y<1 | 当x>0时,y>1 | ||
底数对指数函数的影响:
①在同一坐标系内分别作函数的图象,易看出:当a>l时,底数越大,函数图象在第一象限越靠近y轴;同样地,当0<a<l时,底数越小,函数图象在第一象限越靠近x轴.
②底数对函数值的影响如图.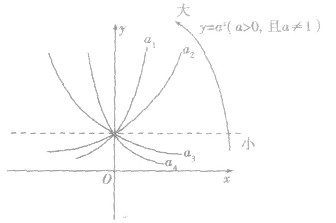
③当a>0,且a≠l时,函数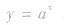 与函数y=
与函数y=![]() 的图象关于y轴对称。
的图象关于y轴对称。
利用指数函数的性质比较大小:
若底数相同而指数不同,用指数函数的单调性比较:
若底数不同而指数相同,用作商法比较;
若底数、指数均不同,借助中间量,同时要注意结合图象及特殊值,
指数函数图象的应用:
函数的图象是直观地表示函数的一种方法.函数的很多性质,可以从图象上一览无余.数形结合就是几何与代数方法紧密结合的一种数学思想.指数函数的图象通过平移、翻转等变可得出一般函数的图象.利用指数函数的图象,可解决与指数函数有关的比较大小、研究单调性、方程解的个数、求值域或最值等问题.
冥函数的定义:
一般地,函数y=xα叫做幂函数,其中x是自变量,α是常数。
幂函数的解析式:
y=xα
幂函数的图像:
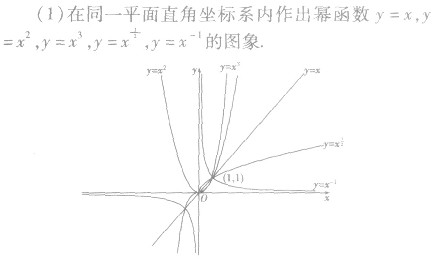
幂函数图像的性质:
所有幂函数在(0,+∞)上都有定义.
①α>0,图像都过定点(0,0)和(1,1);在区间(0,+∞)上单调递增;
②α<0,图像都过定点(1,1);在区间(0,+∞)上单调递减;
③当O<a<l时,曲线上凸,当a>l时,曲线下凸.
④当a=l时,图象为过点(0,0)和(1,1)的直线.
⑤当a=0时, 表示过点(1,1)且平行于x轴的直线(除去点(0,1)) 。
表示过点(1,1)且平行于x轴的直线(除去点(0,1)) 。
幂函数图象的其他性质:
(1)图象的对称性:
把幂函数 的幂指数a(只讨论a是有理数的情况)表示成既约分数的形式(整数看作是分母1的分数),则不论a>0还是a<0,幂函数
的幂指数a(只讨论a是有理数的情况)表示成既约分数的形式(整数看作是分母1的分数),则不论a>0还是a<0,幂函数 的图象的对称性用口诀记为:“子奇母偶孤单单;母奇子偶分两边;分子分母均为奇,原点对称莫忘记”,
的图象的对称性用口诀记为:“子奇母偶孤单单;母奇子偶分两边;分子分母均为奇,原点对称莫忘记”,
(2)图象的形状:
①若a>0,则幂函数 的图象为抛物线形,当a>l时,图象在[0,+∞)上是向下凸的(称为凸函数);当O<a<l时,图象在[o,+∞)上是向上凸的(称为凹函数).
的图象为抛物线形,当a>l时,图象在[0,+∞)上是向下凸的(称为凸函数);当O<a<l时,图象在[o,+∞)上是向上凸的(称为凹函数).
②若a<0,则幂函数y=x“的图象是双曲线形,图象与x轴、y轴无限接近,在(0,+∞)上图象都是向下凸的。
幂函数的单调性和奇偶性:
对于幂函数 (a∈R).
(a∈R).
(1)单调性
当a>0时,函数 在第一象限内是增函数;当a<0时,函数
在第一象限内是增函数;当a<0时,函数 在第一象限内是减函数.
在第一象限内是减函数.
(2)奇偶性
①当a为整数时,
若a为偶数,则 是偶函数;若a为奇数,则
是偶函数;若a为奇数,则 是奇函数。
是奇函数。
②当n为分数,即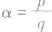 (p,q互素,p,q∈Z)时,若分母q为奇数,则分子p为奇数时,
(p,q互素,p,q∈Z)时,若分母q为奇数,则分子p为奇数时, 为奇函数;分子p为偶数时,
为奇函数;分子p为偶数时, 为偶函数, 若分母q为偶数,则
为偶函数, 若分母q为偶数,则 为非奇非偶函数.
为非奇非偶函数.
与“下列判断正确的是[ ]A.1.72.5>1.73B.0.82<0.83C.D.1.70...”考查相似的试题有:
- 函数f(x)=2|log2x|的图象大致是( ) A. B. C. D.
- 对于,给出下列四个不等式:①;②;③;④其中成立的是[ ]A.①与③B.①与④C.②与③D.②与④
- 已知f(x)=logax,(a>0且a≠1).且当x<0时,ax>1,则f(1-)>1的解集是( ) A.(,+∞) B.(1,) C.(-∞,) D.(1,)
- 直线x=a (a>0) 与函数y=(13)x,y=(12)x,y=2x,y=10x的图象依次交于A、B、C、D四点,则这四点从上到下的排列次序是 __...
- 设a>0,且a≠1,则函数y=ax+1的图像必过的定点坐标是( )。
- 若指数函数y=(a+1)x在(-∞,+∞)上是减函数,那么( ) A.0<a<1 B.-1<a<0 C.a=-1 D.a<-1
- 设a>0,a≠1,函数有最大值,则不等式loga(x2-5x+7)>0的解集为( )。
- 若,则化简的结果是( ) A.B.C.D.
- 给出下列三个等式:f(xy)=f(x)·f(y),f(x+y)=f(x)·f(y),=f(x)-f(y)。下列函数中不满足其中任何一个等式的是...
- 函数的图象是 ( )