返回

高中数学

首页
首页 高中数学知识 指数函数模型的应用 基本不等式及其应用 试题正文
  • 填空题
    函数f（x）=ax-1+3（a＞0，且a≠1）的图象过一个定点P，且点P在直线mx+ny-1=0（m＞0且n＞0）上，则
    1
    m
    +
    4
    n
    的最小值是______．
    本题信息：数学填空题难度一般 来源:未知
  • 本题答案
    查看答案
本试题 “函数f（x）=ax-1+3（a＞0，且a≠1）的图象过一个定点P，且点P在直线mx+ny-1=0（m＞0且n＞0）上，则1m+4n的最小值是______．” 主要考查您对

指数函数模型的应用

基本不等式及其应用

等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
  • 指数函数模型的应用
  • 基本不等式及其应用
指数函数模型的定义：

恰当选择自变量将问题的目标表示成自变量的函数f（x）=a·bx+c（a、b、c为常数，a≠0，b＞0，b≠1）的形式，进而结合指数函数的性质解决问题。

指数型复合函数的性质的应用:

(1)与指数函数有关的复合函数基本上有两类：
；②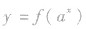.无论是哪一类，要搞清楚复合过程，才能确定复合函数的值域和单调区间，具体问题中，a的取值不定时，要对a进行分类讨论．
(2)对于形如一类的指数型复合函数，有以下结论：
①函数的定义域与f(x)的定义域相同；
②先确定函数f(x)的值域，再根据指数函数的值域、单调性，确定函数的值域；
③当a>l时，函数与函数f(x)的单调性相同；当O<a<l时，函数与函数f(x)的单调性相反.


基本不等式：

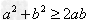（当且仅当a＝b时取“=”号）；
变式：①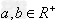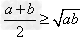，（当且仅当a＝b时取“=”号），即两个正数的算术平均不小于它们的几何平均。
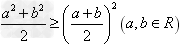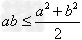②；③；④；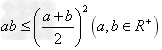


对基本不等式的理解：

(1)基本不等式的证明是利用重要不等式推导的，即，即有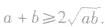
(2)基本不等式又称为均值定理、均值不等式等，其中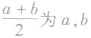的算术平均数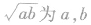，的几何平均数，本定理也可叙述为：两个正数的算术平均数不小于它们的几何平均数．
(3)要特别注意不等式成立的条件和等号成立的条件．均值不等式中：①当a=b时取等号，即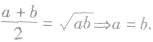


对于两个正数x，y，若已知xy，x+y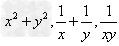，中的某一个为定值，可求出其余各个的最值：
如：（1）当xy＝P（定值），那么当x=y时，和x+y有最小值2，；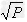
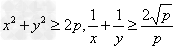（2）x+y=S（定值），那么当x=y时，积xy有最大值，；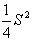
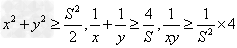（3）已知x2+y2=p，则x+y有最大值为，。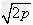

应用基本的不等式解题时：

注意创设一个应用基本不等式的情境及使等号成立的条件，即“一正、二定、三相等”。

利用基本不等式比较实数大小：

(1)注意均值不等式的前提条件．
(2)通过加减项的方法配凑成使用均值定理的形式．
(3)注意“1”的代换．
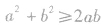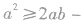
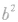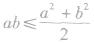(4)灵活变换基本不等式的形式，并注重其变形形式的运用．重要不等式的形式可以是，也可以是，还可以是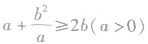等，不仅要掌握原来的形式，还要掌握它的几种变形形式以及公式的逆用等，以便应用．
(5)合理配组，反复应用均值不等式。 


基本不等式的几种变形公式：
 
 

发现相似题
与“函数f（x）=ax-1+3（a＞0，且a≠1）的图象过一个定点P，且点P...”考查相似的试题有：