命题的概念:
1、命题:把语言、符号或式子表达的,可以判断真假的陈述句称为命题;
2、真命题、假命题:判断为真的语句称为真命题,判断为假的语句称为假命题。
注意:
1、并不是所有的语句都是命题,只有能够判断真假的语句才是命题。
2、如果一个语句是命题,则它是真命题或是假命题,二者必具其一。
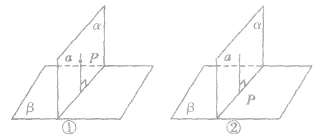
平面和平面垂直的定义:
如果两个平面相交,所成的二面角(从一条直线出发的两个半平面所组成的图形)是直二面角(平面角是直角),就说这两个平面垂直。如图,
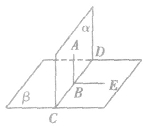
面面垂直的判定定理:
如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直。(线面垂直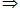 面面垂直)
面面垂直)
面面垂直的性质定理:
如果两个平面互相垂直,那么在一个平面内垂直于他们的交线的直线垂直于另一个平面。(面面垂直 线面垂直)
线面垂直)
性质定理符号表示:
线线垂直、线面垂直、面面垂直的转化关系:
证明面面垂直的方法:
证明两个平面垂直,通常是通过证明线线垂直、线面垂直来实现的,在关于垂直问题的论证中要注意三者之间的相互转化,必要时可添加辅助线,如:已知面面垂直时,一般用性质定理,在一个平面内作出交线的垂线,使之转化为线面垂直,然后转化为线线垂直,故要熟练掌握三者之间的转化条件及常用方法.线面垂直与面面垂直最终归纳为线线垂直,证共面的两直线垂直常用勾股定理的逆定理、等腰三角形的性质;证不共面的两直线垂直通常利用线面垂直或利用空间向量.
常用结论:
(1)如果两个平面互相垂直,那么经过第一个平面内的一点垂直于第二个平面的直线在第一个平面内,此结论可以作为性质定理用,
(2)从该性质定理的条件看出:只要在其中一个平面内通过一点作另一个平面的垂线,那么这条垂线必在这个平面内,点的位置既可以在交线上,也可以不在交线上,如图.