本试题 “已知函数f(x)=32sin2x-cos2x-12,x∈R.(Ⅰ)求函数f(x)的单调递减区间;(Ⅱ)设△ABC的三个内角A,B,C的对边分别为a,b,c,其中c=23,f(C)=0,若向量m...” 主要考查您对已知三角函数值求角
余弦定理
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 已知三角函数值求角
- 余弦定理
反三角函数的定义:
(1)反正弦:在闭区间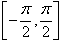 上符合条件sinx=a(-1≤a≤1)的角x,叫做实数a的反正弦,记作arcsina,即x=arcsina,其中x∈
上符合条件sinx=a(-1≤a≤1)的角x,叫做实数a的反正弦,记作arcsina,即x=arcsina,其中x∈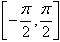 ,且a=sinx;
,且a=sinx;
注意arcsina表示一个角,这个角的正弦值为a,且这个角在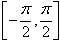 内(-1≤a≤1)。
内(-1≤a≤1)。
(2)反余弦:在闭区间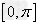 上,符合条件cosx=a(-1≤a≤1)的角x,叫做实数a的反余弦,记作arccosa,即x=arccosa,其中x∈[0,π],且a=cosx。
上,符合条件cosx=a(-1≤a≤1)的角x,叫做实数a的反余弦,记作arccosa,即x=arccosa,其中x∈[0,π],且a=cosx。
(3)反正切:在开区间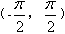 内,符合条件tanx=a(a为实数)的角x,叫做实数a的反正切,记做arctana,即x=arctana,其中x∈
内,符合条件tanx=a(a为实数)的角x,叫做实数a的反正切,记做arctana,即x=arctana,其中x∈ ,且a=tanx。
,且a=tanx。
反三角函数的性质:
(1)sin(arcsina)=a(-1≤a≤1),cos(arccosa)=a(-1≤a≤1),
tan(arctana)=a;
(2)arcsin(-a)=-arcsina,arccos(-a)=π-arccosa,arctan(-a)=-arctana;
(3)arcsina+arccosa=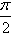 ;
;
(4)arcsin(sinx)=x,只有当x在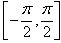 内成立;同理arccos(cosx)=x只有当x在闭区间[0,π]上成立。
内成立;同理arccos(cosx)=x只有当x在闭区间[0,π]上成立。
已知三角函数值求角的步骤:
(1)由已知三角函数值的符号确定角的终边所在的象限(或终边在哪条坐标轴上);
(2)若函数值为正数,先求出对应锐角α1,若函数值为负数,先求出与其绝对值对应的锐角α1;
(3)根据角所在象限,由诱导公式得出0~2π间的角,如果适合条件的角在第二象限,则它是π-α1;如果适合条件的角在第三象限,则它是π+α1;在第四象限,则它是2π-α1;如果是-2π到0的角,在第四象限时为-α1,在第三象限为-π+α1,在第二象限为-π-α1;
(4)如果要求适合条件的所有角,则利用终边相同的角的表达式来写出。
余弦定理:
三角形任意一边的平方等于其他两边的平方的和减去这两边与它们夹角的余弦的积的两倍,
即 。
。
推论:
在△ABC中,若a2+b2=c2,则C为直角;若a2+b2>c2,则C为锐角;若a2+b2<c2,则C为钝角。
余弦定理在解三角形中的应用:
(1)已知两边和夹角,
(2)已知三边。
其它公式:
射影公式: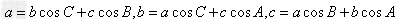
与“已知函数f(x)=32sin2x-cos2x-12,x∈R.(Ⅰ)求函数f(x)的...”考查相似的试题有:
- 已知:tan(π4+a)=15,求sin2a-sin2a1-cos2a的值.
- 已知函数f(x)=1-3sin2x+2cos2x.(1)求f(x)的最大值及取得最大值时的x集合;(2)设△ABC的角A,B,C的对边分别为a,b,c,...
- 若f(cosx)=cos2x,则f(sin15°)=______.
- 在△ABC中角A、B、C的对边分别是a、b、c,若(2b-c)cosA=acosC,则∠A为( )A.π6B.π4C.π3D.5π6
- 如图,甲船以每小时30海里的速度向正北方向航行,乙船按固定方向匀速直线航行。当甲船位于A1处时,乙船位于甲船的北偏西105°...
- 如图,PA切⊙O于点A,割线PBC经过圆心O,OB=PB=1,OA绕点O逆时针旋转60°到OD,则PD的长为( )。
- 在锐角△ABC中,已知角A、B、C所对的边分别为a,b,c,且tanA-tanB=(1+tanAtanB),(1)若c2=a2+b2-ab,求角A、B、C的大小;(2)...
- 在△ABC中,a,b,c分别是A,B,C的对边,A为锐角.已知向量p=(1,3cosA2),q=(2sinA2,1-cos2A),(1)若向量r=(-1,-1),当r...
- 已知△ABC的内角A、B、C所对应边分别为a、b、c,若,则角C的大小是_______________(结果用反三角函数值表示)
- 在△ABC中,内角A,B,C所对边的边长分别是a,b,c.(1)若c=2,C=π3且△ABC的面积等于3,求cos(A+B)和a,b的值;(2)若B是...