本试题 “如图,PA切⊙O于点A,割线PBC经过圆心O,OB=PB=1,OA绕点O逆时针旋转60°到OD,则PD的长为( )。” 主要考查您对余弦定理
圆的切线的性质及判定定理
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 余弦定理
- 圆的切线的性质及判定定理
余弦定理:
三角形任意一边的平方等于其他两边的平方的和减去这两边与它们夹角的余弦的积的两倍,
即 。
。
推论:
在△ABC中,若a2+b2=c2,则C为直角;若a2+b2>c2,则C为锐角;若a2+b2<c2,则C为钝角。
余弦定理在解三角形中的应用:
(1)已知两边和夹角,
(2)已知三边。
其它公式:
射影公式: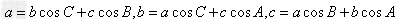
圆的相切的定义:
直线和圆只有一个公共点,即圆心到直线的距离等于半径,这条直线叫圆的切线。
切线的性质定理:
圆的切线垂直于经过切点的半径。
推论1:
经过圆心且垂直于切线的直线必经过切点;
推论2:
经过切点且垂直于切线的直线必经过圆心。
切线的判定定理:
经过半径的外端并且垂直于这条半径的直线是圆的切线。
直线与圆的位置关系:
相离:直线和圆没有公共点,即圆心到直线的距离大于半径;
相交:直线和圆有两个公共点,即圆心到直线的距离小于半径,这条直线叫圆的割线;
相切:直线和圆只有一个公共点,即圆心到直线的距离等于半径,这条直线叫圆的切线。
发现相似题
与“如图,PA切⊙O于点A,割线PBC经过圆心O,OB=PB=1,OA绕点O逆时...”考查相似的试题有:
- 在三角形ABC中,若,则bc的最大值是( )。
- 在△ABC中,已知a=5,b=3,C=120°,则c=( )A.8B.7C.6D.5
- 在△ABC中,内角A,B,C所对的边分别为a,b,c.向量且满足.(1)求角C的大小;(2)若求△ABC的面积.
- 在△ABC中,已知a=2,b=2,c=3+1,求A.
- 在△ABC中,角A,B,C所对的边分别为a,b,c,若3bcosA=ccosA+acosC,则tanA的值是( )A.-22B.-2C.22D.2
- 已知△ABC中,角A、B、C所对的边分别为a、b、c,且tanA=34.(I)求sin2B+C2+cos2A的值;(II)若△ABC的面积S=3,且b=2,求△AB...
- 在△ABC中,角A、B、C的对边分别为a、b、c,如果,那么三边长a、b、c之间满足的关系是( )A. B. C. D.
- 在△ABC中,角A,B,C的对边分别是a,b,c,且b2=ac=a2-c2+bc,(1)求的值;(2)试判断△ABC的形状,并说明理由。
- 已知双曲线的离心率为,左、右焦点分别为、,一条准线的方程为.(1)求双曲线的方程;(2)若双曲线上的一点满足,求的值;(...
- 如图,AB是⊙O的直径,⊙O交BC的中点与D,DE⊥AC.(1)求证:△BAD∽△CED;(2)求证:DE是⊙O的切线.