本试题 “已知正项数列{an}的前项和为Sn,且满足.(Ⅰ)求证:数列{an}是等差数列;(Ⅱ)设;(Ⅲ)设,求证:.” 主要考查您对等差数列的定义及性质
数列求和的其他方法(倒序相加,错位相减,裂项相加等)
不等式的定义及性质
基本不等式及其应用
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 等差数列的定义及性质
- 数列求和的其他方法(倒序相加,错位相减,裂项相加等)
- 不等式的定义及性质
- 基本不等式及其应用
等差数列的定义:
一般地,如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫做等差数列,这个常数叫做公差,用符号语言表示为an+1-an=d。
等差数列的性质:
(1)若公差d>0,则为递增等差数列;若公差d<0,则为递减等差数列;若公差d=0,则为常数列;
(2)有穷等差数列中,与首末两端“等距离”的两项和相等,并且等于首末两项之和;
(3)m,n∈N*,则am=an+(m-n)d;
(4)若s,t,p,q∈N*,且s+t=p+q,则as+at=ap+aq,其中as,at,ap,aq是数列中的项,特别地,当s+t=2p时,有as+at=2ap;
(5)若数列{an},{bn}均是等差数列,则数列{man+kbn}仍为等差数列,其中m,k均为常数。
(6)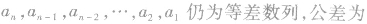
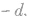
(7)从第二项开始起,每一项是与它相邻两项的等差中项,也是与它等距离的前后两项的等差中项,即

(8)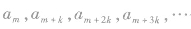 仍为等差数列,公差为
仍为等差数列,公差为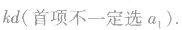
对等差数列定义的理解:
①如果一个数列不是从第2项起,而是从第3项或某一项起,每一项与它前一项的差是同一个常数,那么此数列不是等差数列,但可以说从第2项或某项开始是等差数列.
②求公差d时,因为d是这个数列的后一项与前一项的差,故有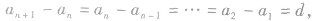 还有
还有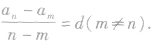
③公差d∈R,当d=0时,数列为常数列(也是等差数列);当d>0时,数列为递增数列;当d<0时,数列为递减数列;
④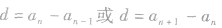 是证明或判断一个数列是否为等差数列的依据;
是证明或判断一个数列是否为等差数列的依据;
⑤证明一个数列是等差数列,只需证明an+1-an是一个与n无关的常数即可。
等差数列求解与证明的基本方法:
(1)学会运用函数与方程思想解题;
(2)抓住首项与公差是解决等差数列问题的关键;
(3)等差数列的通项公式、前n项和公式涉及五个量:a1,d,n,an,Sn,知道其中任意三个就可以列方程组求出另外两个(俗称“知三求二’).
数列求和的常用方法:
1.裂项相加法:数列中的项形如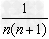 的形式,可以把
的形式,可以把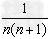 表示为
表示为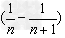 ,累加时抵消中间的许多项,从而求得数列的和;
,累加时抵消中间的许多项,从而求得数列的和;
2、错位相减法:源于等比数列前n项和公式的推导,对于形如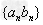 的数列,其中
的数列,其中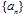 为等差数列,
为等差数列,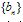 为等比数列,均可用此法;
为等比数列,均可用此法;
3、倒序相加法:此方法源于等差数列前n项和公式的推导,目的在于利用与首末两项等距离的两项相加有公因式可提取,以便化简后求和。
4、分组转化法:把数列的每一项分成两项,或把数列的项“集”在一块重新组合,或把整个数列分成两个部分,使其转化为等差或等比数列,这一求和方法称为分组转化法。
5、公式法求和:所给数列的通项是关于n的多项式,此时求和可采用公式求和,常用的公式有:
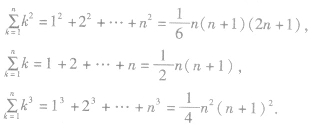
数列求和的方法多种多样,要视具体情形选用合适方法。
数列求和特别提醒:
(1)对通项公式含有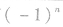 的一类数列,在求
的一类数列,在求 时,要注意讨论n的奇偶性;
时,要注意讨论n的奇偶性;
(2)在用等比数列前n项和公式时,一定要分q=1和q≠1两种情况来讨论。
不等式的定义:
一般地,用不等号表示不相等关系的式子叫做不等式,常见的不等号有“<”“>”“ ≤”“≥”及“≠”。
严格不等式的定义:
用“>"“<”连接的不等式叫做严格不等式。
非严格不等式的定义:
用“≤”和“≥”连接的不等式叫做非严格不等式.
特别提醒:a=b,a>b中,只要有一个成立,就有a≥b.
不等式的性质:
(1)如果a>b,那么b<a;如果b<a,那么a>b,即a>b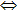 b<a;
b<a;
(2)如果a>b,b>c,那么a>c,即a>b,b>c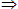 a>c;
a>c;
(3)如果a>b,那么a+c>b+c;
(4)如果a>b,c>0,那么ac>bc;如果a>b,c<0,那么ac<bc;
(5)如果a>b,c>d,那么a+c>b+d;
(6)如果a>b>0,c>d>0,那么ac>bd;
(7)如果a>b>0,那么an>bn(n∈N,n≥2);
(8)如果a>b>0,那么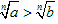 (n∈N,n≥2)。
(n∈N,n≥2)。
不等关系与不等式的区别:
不等关系强调的是量与量之间的关系,可以用符号“<…>…≤”“≥”来表示,也可以用语言表述;
而不等式则是用来表示不等关系的式子,可用“a>b”‘a<b”“a≥b a≤b”等式子来表示,不等关系是通过不等式来体现的.
不等式的分类:
①按成立的条件分:a.绝对不等式:不等式中的字母取任意实数值都恒成立的不等式叫做绝对不等式;b.条件不等式:不等式中的字母取某些允许值才能成立的不等式叫做条件不等式;c.矛盾不等式:不等式中的字母不论取何实数值都不能成立的不等式叫做矛盾不等式;
②按不等号开口方向分:a.同向不等式:不等号方向相同的两个不等式;b.异向不等式:不等号方向相反的两个不等式.
基本不等式:
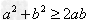 (当且仅当a=b时取“=”号);
(当且仅当a=b时取“=”号);
变式:①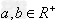 ,
,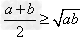 (当且仅当a=b时取“=”号),即两个正数的算术平均不小于它们的几何平均。
(当且仅当a=b时取“=”号),即两个正数的算术平均不小于它们的几何平均。
②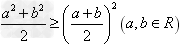 ;③
;③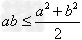 ;④
;④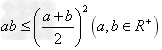 ;
;
对基本不等式的理解:
(1)基本不等式的证明是利用重要不等式推导的,即 ,即有
,即有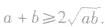
(2)基本不等式又称为均值定理、均值不等式等,其中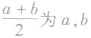 的算术平均数,
的算术平均数,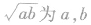 的几何平均数,本定理也可叙述为:两个正数的算术平均数不小于它们的几何平均数.
的几何平均数,本定理也可叙述为:两个正数的算术平均数不小于它们的几何平均数.
(3)要特别注意不等式成立的条件和等号成立的条件.均值不等式中:①当a=b时取等号,即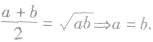
对于两个正数x,y,若已知xy,x+y,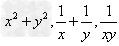 中的某一个为定值,可求出其余各个的最值:
中的某一个为定值,可求出其余各个的最值:
如:(1)当xy=P(定值),那么当x=y时,和x+y有最小值2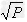 ,
,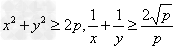 ;
;
(2)x+y=S(定值),那么当x=y时,积xy有最大值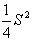 ,
,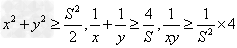 ;
;
(3)已知x2+y2=p,则x+y有最大值为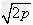 ,
, 。
。
应用基本的不等式解题时:
注意创设一个应用基本不等式的情境及使等号成立的条件,即“一正、二定、三相等”。
利用基本不等式比较实数大小:
(1)注意均值不等式的前提条件.
(2)通过加减项的方法配凑成使用均值定理的形式.
(3)注意“1”的代换.
(4)灵活变换基本不等式的形式,并注重其变形形式的运用.重要不等式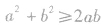 的形式可以是
的形式可以是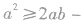
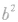 ,也可以是
,也可以是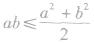 ,还可以是
,还可以是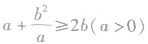 等,不仅要掌握原来的形式,还要掌握它的几种变形形式以及公式的逆用等,以便应用.
等,不仅要掌握原来的形式,还要掌握它的几种变形形式以及公式的逆用等,以便应用.
(5)合理配组,反复应用均值不等式。

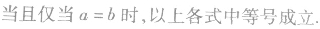
与“已知正项数列{an}的前项和为Sn,且满足.(Ⅰ)求证:数列{an}...”考查相似的试题有:
- 已知等比数列为递增数列,且,.(Ⅰ)求;(Ⅱ)令,不等式的解集为,求所有的和.
- (本小题满分14分)已知等差数列的公差大于0,且是方程的两根,数列的前项的和为,且.(1)求数列,的通项公式;(2)记,求证...
- 数列{an}前n项和为Sn,点(n,Sn)在抛物线y=x2+1上.(1)试写出数列{an}的前5项;(2)数列{an}是等差数列吗?试证明你的结...
- 已知等差数列{an}的公差为2,若a1,a3,a4成等比数列,则a2=( )A.-4B.-6C.-8D.-10
- 在数列{}中,若对任意的n均有++为定值,且,,则数列的前100项的和S100= ( )A.132B.299C.68D.99
- 已知数列{an}满足3an+1+an=4(n∈N*)且a1=9,其前n项和为Sn,则满足不等式|Sn-n-6|<1125的最小整数n是( )A.5B.6C.7D.8
- 已知函数,若存在正常数,使,则不等式的解集是_________。
- 已知满足,则下列选项成立的是( )A.B.C.D.
- 已知y=f(x)是偶函数,当x>0时,,且当x∈[-3,-1]时,n≤f(x)≤m恒成立,则n-m的最大值是( )
- 设OA=(1,-2),OB=(a,-1),OC=(-b,0)且a≥0,b≥0,O为坐标原点,若A、B、C三点共线,则4a+21+b的最小值为______.