已知曲线x216-m-y2m=1．（1）当曲线是椭圆时，求m的取值范围，并写出焦点坐标；（2）当曲线是双曲线时，求m的取值范围，并写出焦点坐,高中,数学试题,椭圆的定义考点,双曲线的定义考点,好技网

本试题 “已知曲线x216-m-y2m=1．（1）当曲线是椭圆时，求m的取值范围，并写出焦点坐标；（2）当曲线是双曲线时，求m的取值范围，并写出焦点坐标．” 主要考查您对
椭圆的定义

双曲线的定义
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。

椭圆的第一定义：

平面内与两个定点为F₁，F₂的距离的和等于常数（大于）的轨迹叫做椭圆，这两个定点叫做椭圆的焦点，两焦点的距离叫做椭圆的焦距。特别地，当常数等于时，轨迹是线段F₁F₂，当常数小于时，无轨迹。

椭圆的第二定义：

平面内到定点F的距离和到定直线l的距离之比等于常数e（0＜e＜1）的点的轨迹，叫做椭圆，定点F叫椭圆的焦点，定直线l叫做椭圆的准线，e叫椭圆的离心率。

椭圆的定义应该包含几个要素：

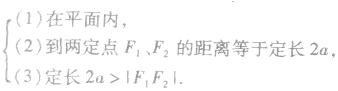
利用椭圆的定义解题：

当题目中出现一点在椭圆上的条件时，注意使用定义

双曲线第一定义：

平面内与两定点F₁，F₂的距离的差的绝对值等于定长2a（小于|F₁F₂|）的点的轨迹叫双曲线，即||PF₁|-|PF₂||=2a（2a＜|F₁F₂|）。若2a＝|F₁F₂|，则轨迹是以F₁，F₂为端点射线，若2a＞|F₁F₂|，则轨迹不存在；若去掉定义中的绝对值则轨迹仅表示双曲线的一支。

双曲线的第二定义：

平面内与一个定点F和一条定直线l的距离的比是常数e（e＞1）的动点的轨迹叫双曲线。

双曲线的理解：

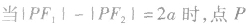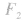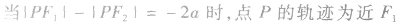的轨迹为近的一支；的一支。
注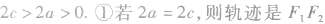：的延长线和反向延长线（两条射线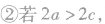）；则轨迹不存在；的垂直平分线。

发现相似题

与“已知曲线x216-m-y2m=1．（1）当曲线是椭圆时，求m的取值范围...”考查相似的试题有：