本试题 “在平面直角坐标系中,已知向量a=(-1,2),又点A(8,0),B(-8,t),C(8sinθ,t).(I)若AB⊥a求向量OB的坐标;(Ⅱ)若向量AC与向量a共线,当tsinθ取最...” 主要考查您对平面向量基本定理及坐标表示
用数量积判断两个向量的垂直关系
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 平面向量基本定理及坐标表示
- 用数量积判断两个向量的垂直关系
平面向量的基本定理:
如果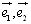 是同一平面内的两个不共线的向量,那么对这一平面内的任一向量
是同一平面内的两个不共线的向量,那么对这一平面内的任一向量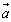 存在唯一的一对有序实数
存在唯一的一对有序实数 使
使 成立,不共线向量
成立,不共线向量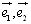 表示这一平面内所有向量的一组基底。
表示这一平面内所有向量的一组基底。
平面向量的坐标运算:
在平面内建立直角坐标系,以与x轴、y轴方向相同的两个单位向量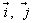 为基底,则平面内的任一向量
为基底,则平面内的任一向量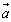 可表示为
可表示为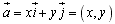 ,称(x,y)为向量
,称(x,y)为向量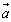 的坐标,
的坐标,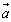 =(x,y)叫做向量
=(x,y)叫做向量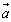 的坐标表示。
的坐标表示。
基底在向量中的应用:
(l)用基底表示出相关向量来解决向量问题是常用的方法之一.
(2)在平面中选择基底主要有以下几个特点:①不共线;②有公共起点;③其长度及两两夹角已知.(3)用基底表示向量,就是利用向量的加法和减法对有关向量进行分解。
用已知向量表示未知向量:
用已知向量表示未知向量,一定要结合图像,可从以下角度如手:
(1)要用基向量意识,把有关向量尽量统一到基向量上来;
(2)把要表示的向量标在封闭的图形中,表示为其它向量的和或差的形式,进而寻找这些向量与基向量的关系;
(3)用基向量表示一个向量时,如果此向量的起点是从基底的公共点出发的,一般考虑用加法,否则用减法,如果此向量与一个易求向量共线,可用数乘。
两向量垂直的充要条件:
非零向量 ,那么
,那么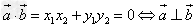 ,所以可以根据此公式判断两个向量是否垂直。
,所以可以根据此公式判断两个向量是否垂直。
向量数量积的性质:
设两个非零向量
(1) ;
;
(2) ;
;
(3) ;
;
(4) ;
;
(5)当 ,
, 同向时,
同向时, ;当
;当 与
与 反向时,
反向时, ;当
;当 为锐角时,
为锐角时, 为正且
为正且 ,
, 不同向,
不同向, ;当
;当 为钝角时,
为钝角时, 为负且
为负且 ,
, 不反向,
不反向, 。
。
发现相似题
与“在平面直角坐标系中,已知向量a=(-1,2),又点A(8,0),B...”考查相似的试题有:
- 已知向量a=(1,x),b=(2,1).若向量λa-b与a+3b平行,则实数λ=______.
- 下列向量组中,能作为平面内所有向量基底的是( )A.e1=(0,0),e2=(1,-2)B.e1=(-1,2),e2=(5,7)C.e1=(3,5)...
- 已知四面体A—BCD,设,,,,E、F分别为AC、BD中点,则可用表示为__ _____ ____.
- 已知且∥,则= .
- 已知a=(3,x),b=(2,x-1),若a∥b,则x的值为( )A.3B.-3C.2D.-2
- 若向量BA=(2,3),CA=(4,7),则BC=______.
- 设向量,,则下列结论中正确的是( )A.B.C.与垂直D.∥
- 已知点A(-1,1),点B(2,y),向量a=(1,2),若AB∥a,则实数y的值为( )A.5B.6C.7D.8
- 已知向量,,且(1)求的取值范围;(2)求函数的最小值,并求此时x的值
- 已知向量a=(1,y),b=(1,-3),且(2a+b)⊥b.(1)求|a|;(2)若(ka+2b)∥(2a-4b),求k的值.