本试题 “已知函数f(x)=ax的图象过点(1,),且点(n-1,)(n∈N*)在函数f(x)=ax的图象上。(1)求数列{an}的通项公式;(2)令bn=an+1-an,若数列{bn}的前n项和...” 主要考查您对指数函数的图象与性质
一般数列的通项公式
数列求和的其他方法(倒序相加,错位相减,裂项相加等)
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 指数函数的图象与性质
- 一般数列的通项公式
- 数列求和的其他方法(倒序相加,错位相减,裂项相加等)
指数函数y=ax(a>0,且a≠1)的图象和性质:
| 0<a<1 | a>1 | ||
| 图像 | 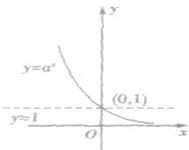 |
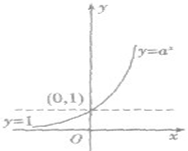 | |
| 图像 | 定义域 | R | |
| 值域 | (0,+∞) | ||
| 恒过定点 | 图像恒过定点(0,1),即当x等于0时,y=1 | ||
| 单调性 | 在(-∞,+∞)上是减函数 | 在(-∞,+∞)上是增函数 | |
| 函数值的变化规律 | 当x<0时,y>1 | 当x<0时,0<y<1 | |
| 当x=0时,y=1 | 当x=0时,y=1 | ||
| 当x>0时,0<y<1 | 当x>0时,y>1 | ||
底数对指数函数的影响:
①在同一坐标系内分别作函数的图象,易看出:当a>l时,底数越大,函数图象在第一象限越靠近y轴;同样地,当0<a<l时,底数越小,函数图象在第一象限越靠近x轴.
②底数对函数值的影响如图.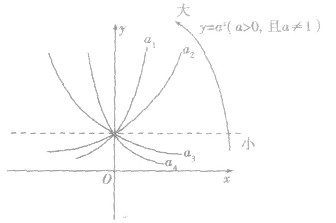
③当a>0,且a≠l时,函数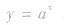 与函数y=
与函数y=![]() 的图象关于y轴对称。
的图象关于y轴对称。
利用指数函数的性质比较大小:
若底数相同而指数不同,用指数函数的单调性比较:
若底数不同而指数相同,用作商法比较;
若底数、指数均不同,借助中间量,同时要注意结合图象及特殊值,
指数函数图象的应用:
函数的图象是直观地表示函数的一种方法.函数的很多性质,可以从图象上一览无余.数形结合就是几何与代数方法紧密结合的一种数学思想.指数函数的图象通过平移、翻转等变可得出一般函数的图象.利用指数函数的图象,可解决与指数函数有关的比较大小、研究单调性、方程解的个数、求值域或最值等问题.
一般数列的定义:
如果数列{an}的第n项an与序号n之间的关系可以用一个式子表示成an=f(n),那么这个公式叫做这个数列的通项公式。
通项公式的求法:
(1)构造等比数列:凡是出现关于后项和前项的一次递推式都可以构造等比数列求通项公式;
(2)构造等差数列:递推式不能构造等比数列时,构造等差数列;
(3)递推:即按照后项和前项的对应规律,再往前项推写对应式。
已知递推公式求通项常见方法:
①已知a1=a,an+1=qan+b,求an时,利用待定系数法求解,其关键是确定待定系数λ,使an+1 +λ=q(an+λ)进而得到λ。
②已知a1=a,an=an-1+f(n)(n≥2),求an时,利用累加法求解,即an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)的方法。
③已知a1=a,an=f(n)an-1(n≥2),求an时,利用累乘法求解。
数列求和的常用方法:
1.裂项相加法:数列中的项形如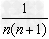 的形式,可以把
的形式,可以把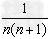 表示为
表示为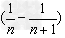 ,累加时抵消中间的许多项,从而求得数列的和;
,累加时抵消中间的许多项,从而求得数列的和;
2、错位相减法:源于等比数列前n项和公式的推导,对于形如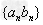 的数列,其中
的数列,其中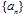 为等差数列,
为等差数列,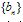 为等比数列,均可用此法;
为等比数列,均可用此法;
3、倒序相加法:此方法源于等差数列前n项和公式的推导,目的在于利用与首末两项等距离的两项相加有公因式可提取,以便化简后求和。
4、分组转化法:把数列的每一项分成两项,或把数列的项“集”在一块重新组合,或把整个数列分成两个部分,使其转化为等差或等比数列,这一求和方法称为分组转化法。
5、公式法求和:所给数列的通项是关于n的多项式,此时求和可采用公式求和,常用的公式有:
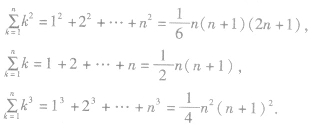
数列求和的方法多种多样,要视具体情形选用合适方法。
数列求和特别提醒:
(1)对通项公式含有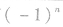 的一类数列,在求
的一类数列,在求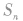 时,要注意讨论n的奇偶性;
时,要注意讨论n的奇偶性;
(2)在用等比数列前n项和公式时,一定要分q=1和q≠1两种情况来讨论。
与“已知函数f(x)=ax的图象过点(1,),且点(n-1,)(n∈N*)...”考查相似的试题有:
- 给出下列三个等式:f(xy)=f(x)+f(y),f(x+y)=f(x)f(y),f(x+y)=f(x)+f(y),则下列函数中不满足其中任何一个等式的是[ ]A.f(x...
- 已知数列{an},对于任意n≥2,在an-1与an之间插入n个数,构成的新数列{bn}成等差数列,并记在an-1与an之间插入的这n个数均值为...
- 已知数列{an},满足a1=1,an=a1+2a2+3a3+…+(n-1)an-1(n≥2),则{an}的通项。
- 已知数列{an}中,a1=8,a4=2满足an+2-2an+1+an=0(n∈N*),(1)求数列{an}的通项公式;(2)设Sn=|a1|+|a2|+…+|an|,求Sn;...
- 求和12-22+32-42+…+992-1002.
- 数列{an}中,a1=1,a2=4,an=2n-1+λn2+μn,(n∈N*).(Ⅰ)求λ、μ的值;(Ⅱ)设数列{bn}满足:bn=1an+2n-2n-1,求数列{bn}的...
- 已知数列{an}和{bn}满足:a1=1,a2=2,an>0,bn=anan+1(n∈N*),且{bn}是以q为公比的等比数列.(I)证明:an+2=anq2;(II...
- 已知等差数列{an}的前三项为a-1,4,2a,记前n项和为Sn.(Ⅰ)设Sk=2550,求a和k的值;(Ⅱ)设bn=Snn,求b3+b7+b11+…+b4n-1的...
- 已知二次函数同时满足:①不等式的解集有且只有一个元素;②在定义域内存在,使得不等式成立.数列的通项公式为.(1)求函数的表...
- 设等差数列{an}的前n项和为Sn,且a2=4,S5=30.数列{bn}满足b1=0,bn=2bn-1+1,(n∈N,n≥2),①求数列{an}的通项公式;②设Cn=...