本试题 “已知数列{an}的前n项和为Sn,且a1=1,a2=3,2Sn﹣(n+1)an=An+B(其中A、B是常数,n∈N*).(1)求A、B的值;(2)求证数列是等差数列,并求数列{an}的通项...” 主要考查您对等差数列的通项公式
等差数列的前n项和
一元二次不等式及其解法
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 等差数列的通项公式
- 等差数列的前n项和
- 一元二次不等式及其解法
等差数列的通项公式:
an=a1+(n-1)d,n∈N*。
an=dn+a1-d,d≠0时,是关于n的一次函数,斜率为公差d;
an=kn+b(k≠) {an}为等差数列,反之不能。
{an}为等差数列,反之不能。
对等差数列的通项公式的理解:
①从方程的观点来看,等差数列的通项公式中含有四个量,只要已知其中三个,即可求出另外一个.其中a1和d是基本量,只要知道a1和d即可求出等差数列的任一项;
②从函数的观点来看,在等差数列的通项公式中,。。是n的一次函数,其图象是直线y=dx+(a1-d)上均匀排开的一列孤立点,我们知道两点确定一条直线,因此,给出一个等差数列的任意两项,等差数列就被唯一确定了,
等差数列公式的推导:
等差数列的通项公式可由 归纳得出,当然,等差数列的通项公式也可用累加法得到:
归纳得出,当然,等差数列的通项公式也可用累加法得到:
等差数列的前n项和的公式:
(1)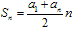 ,(2)
,(2)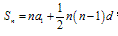 ,(3)
,(3)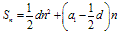 ,(4)
,(4)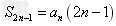
当d≠0时,Sn是关于n的二次函数且常数项为0,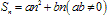
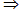 {an}为等差数列,反之不能。
{an}为等差数列,反之不能。
等差数列的前n项和的有关性质:
(1) ,…成等差数列;
,…成等差数列;
(2){an}有2k项时,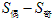 =kd;
=kd;
(3){an}有2k+1项时,S奇=(k+1)ak+1=(k+1)a平, S偶=kak+1=ka平,S奇:S偶=(k+1):k,S奇-S偶=ak+1=a平;
解决等差数列问题常用技巧:
1、等差数列中,已知5个元素:a1,an,n,d, S中的任意3个,便可求出其余2个,即知3求2。
为减少运算量,要注意设元的技巧,如奇数个成等差,可设为…,a-2d,a-d,a,a+d,a+2d,…,偶数个成等差,可设为…,a-3d,a-d,a+d,a+3d,…
2、等差数列{an}中,(1)若ap=q,aq=p,则列方程组可得:d=-1,a1=p+q-1,ap+q=0,S=-(p+q);
(2)当Sp=Sq时(p≠q),数形结合分析可得Sn中最大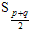 ,Sp+q=0,此时公差d<0。
,Sp+q=0,此时公差d<0。
一元二次不等式的概念:
只含有一个未知数,并且未知数的最高次数是2 的不等式称为一元二次不等式.
一元二次不等式的解集:
使某个一元二次不等式成立的x的值叫做这个一元二次不等式的解,一元二次不等式的所有解组成的集合叫做这个一元二次不等式的解集。
同解不等式:
如果两个不等式的解集相同,那么这两个不等式叫做同解不等式,如果一个不等式变形为另一个不等式时,这两个不等式是同解不等式,那么这种变形叫做不等式的同解变形。
二次函数的图象、一元二次方程的根、一元二次不等式的解集间的关系:
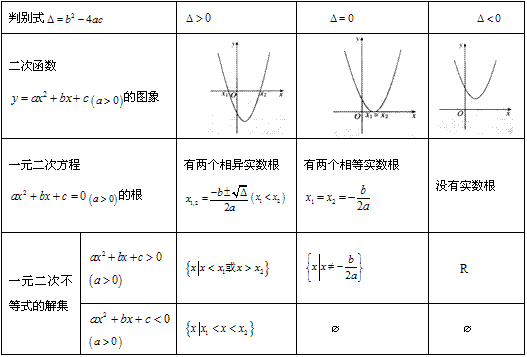
解不等式的过程:
解不等式的过程就是将不等式进行同解变形,化为最简形式的同解不等式的过程.变形时要注意条件的限制,比如:分母是否有意义,定义域是否有限制等.
解一元二次不等式的一般步骤为:
(1)对不等式变形,使一端为零且二次项系数大于零;(2)计算相应的判别式;(3)当△≥0时,求出相应的一元二次方程的根;(4)根据二次函数图象写出一元二次不等式的解集.
解含有参数的一元二次不等式:
(1)要以二次项系数与零的大小作为分类标准进行分类讨论;(2)转化为标准形式的一元二次不等式(即二次项系数大于零)后,再以判别式与零的大小作为分类标准进行分类讨论;(3)如果判别式大于零,但两根的大小还不能确定,此时再以两根的大小作为分类标准进行分类讨论。
与“已知数列{an}的前n项和为Sn,且a1=1,a2=3,2Sn﹣(n+1)an=A...”考查相似的试题有:
- 《莱因德纸草书》( Rhind Papyrus )是世界上最古老的数学著作之一. 书中有一道这样的题目:把100个面包分给5个人,使每个...
- 已知各项均为正数的数列{an}的前n项和sn满足s1>1,且6sn=(an+1)(an+2)(n为正整数).(1)求{an}的通项公式;(2)设数...
- 在等差数列{an}中,a2+a3=7,a4+a5+a6=18.(1)求数列{an}的通项公式;(2)设数列{an}的前n项和为Sn,求.
- 设{an} 是各项均为正整数的等差数列,项数为奇数,公差不为0,且各项之和等于2010,则该数列的第8项a8的值等于______.
- 等差数列{an}的前5项的和为30,前10项的和为100,则它的前15的和为( )A.30B.170C.210D.260
- 已知等差数列{an}中,a2=6,a5=15,若bn=a2n,则数列{bn}的前5项和等于______.
- 在等差数列{an}中,S10=120,那么a1+a10的值是( ) A.12 B.24 C.36 D.48
- 关于x的不等式x2-ax-20a2
- 若不等式-2<x<-14是不等式ax2+bx-2>0成立的充要条件,则实数a,b的值分别为( )A.-8,-10B.-4,-9C.-1,9D.-1,2
- 不等式x2+2x<ab+16ba对任意a,b∈(0,+∞)恒成立,则实数x的取值范围是( )A.(-2,0)B.(-∞,-2)∪(0,+∞)C.(-4,2...