本试题 “(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)A.(不等式选做题)不等式|x-5|+|x+3|≥10的解集是______.B.(坐标系与参数方...” 主要考查您对绝对值不等式
与圆有关的比例线段
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 绝对值不等式
- 与圆有关的比例线段
绝对值不等式:
当a>0时,有 ;
;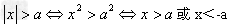 或x<-a 。
或x<-a 。
绝对值不等式的解法:
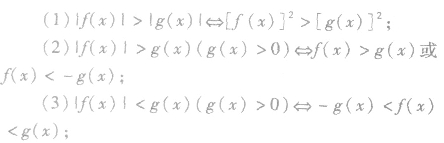
(4)含两个或两个以上绝对值符号的不等式可用零点分区间的方法去绝对值符号求解,也可以用图象法求解。
相交弦定理:
圆内的两条相交弦,被交点分成的两条线段长的积相等。
割线定理:
从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段的长的积相等。
割线长定理:
从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项。
切线长定理:
从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。
应用相交弦定理、切割线定理及推论的证明题的解决方法较多,常见的有:
(1)找过渡乘积式证明等积式成立;
(2)为三角形相似提供对应边成比例的条件;
(3)利用等积式来证明有关线段相等
相交弦定理、切割线定理及它们的推论和切线长定理的应用:
相交弦定理、切割线定理及它们的推论和切线长定理一样,揭示了和圆有关的一些线段间的数量关系,这些定理的证明及应用又常常和相似三角形联系在一起,因此在解题中要善于观察图形,对复杂的图形进行分解,找出基本图形和结论,从而准确地解决问题.另外在和圆有关的比例线段的计算问题中,要注意方程的思想的运用
发现相似题
与“(考生注意:请在下列三题中任选一题作答,如果多做,则按所...”考查相似的试题有:
- 对于实数,若,则的最大值为( )A.4B.6C.8D.10
- 解不等式|x2-9|≤x+3.
- 设函数f(x)=|x-4|+|x-a|(a<4).(Ⅰ)若f(x)的最小值为3,求a值;(Ⅱ)求不等式f(x)≥3-x的解集.
- 已知:全集I=R,集合M={x||x-2|>1},集合N={x|lg(x2+5)=lg6x},求:∁IM∩N=______.
- 不等式|2x-1|<|x-2|的解集为( )。
- 已知集合A={x||x-1|>2},B={x|x(x-5)<0},则A∩B=______.
- 设函数.(1)解不等式;(2)若对一切实数均成立,求的取值范围.
- 如图,圆O的圆心O在Rt△ABC的直角边BC上,该圆与直角边AB相切,与斜边AC交于D,E,AD=DE=EC,AB=14.(Ⅰ)求BC的长;(Ⅱ)求圆...
- 从⊙O外一点P引圆的两条切线PA,PB及一条割线PCD,A、B为切点.求证:ACBC=ADBD.
- (1)已知矩阵M=20012,矩阵M对应的变换把曲线y=x2变为曲线C,求C的方程.(2)已知a,b,c为正实数,求证:1a3+1b3+1c3+abc≥...