本试题 “已知f(x)=ax+b(a>0且a≠1,b为常数)的图象经过点(1,1)且0<f(0)<1,记m=12[f-1(x1)+f-1(x2)],n=f-1(x1+x22)(x1、x2是两个不相等的正实数),试比...” 主要考查您对对数函数的解析式及定义(定义域、值域)
反函数
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 对数函数的解析式及定义(定义域、值域)
- 反函数
对数函数的定义:
一般地,我们把函数y=logax(a>0,且a≠1)叫做对数函数,其中x是自变量,函数的定义域是(0,+∞),值域是R。
对数函数的解析式:
y=logax(a>0,且a≠1)
在解有关对数函数的解析式时注意:
在涉及到对数函数时,一定要注意定义域,即满足真数大于零;求值域时,还要考虑底数的取值范围。
定义:
设式子y=f(x)表示y是x的函数,定义域为A,值域为C,从式子y=f(x)中解出x,得到式子x=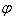 (y),如果对于y在C中的任何一个值,通过式子x=
(y),如果对于y在C中的任何一个值,通过式子x=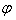 (y),x在A中都有唯一确定的值和它对应,那么式子x=
(y),x在A中都有唯一确定的值和它对应,那么式子x=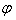 (y)就表示y是x的函数,这样的函数叫做y=f(x)的反函数,记作x=f-1(y),即x=
(y)就表示y是x的函数,这样的函数叫做y=f(x)的反函数,记作x=f-1(y),即x=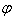 (y)=f-1(y),一般对调x=f-1(y)中的字母x,y,把它改写成y=f-1(x)。
(y)=f-1(y),一般对调x=f-1(y)中的字母x,y,把它改写成y=f-1(x)。
反函数的一些性质:
(1)反函数的定义域和值域分别是原函数的值域和定义域,称为互调性;
(2)定义域上的单调函数必有反函数,且单调性相同(即函数与其反函数在各自的定义域上的单调性相同),对连续函数而言,只有单调函数才有反函数,但非连续的非单调函数也可能有反函数;
(3)函数y=f(x)的图象与其反函数y=f-1(x)的图象关于直线y=x对称,但要注意:函数y=f(x)的图象与其反函数x= (y)=f-1(y)的图象相同。(对称性)
(y)=f-1(y)的图象相同。(对称性)
(4)设y=f(x)与y=g(x)互为反函数,如果点(a,b)在函数y=f(x)的图像上,那么点(b,a)在它的反函数y=g(x)的图像上。
(5)函数y=f(x)的反函数是y=f-1(x),函数y=f-1(x )的反函数是y=f(x),称为互反性,但要特别注意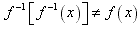 ;
;
(6)函数y=f(x)的图象与其反函数y=f-1(x)的图象的交点,当它们是递增时,交点在直线y=x上。当它们递减时,交点可以不在直线y=x上,
如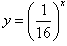 与
与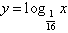 互为反函数且有一个交点是
互为反函数且有一个交点是 ,它不再直线y=x上。
,它不再直线y=x上。
(7)还原性: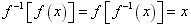 。
。
求反函数的步骤:
(1)将y=f(x)看成方程,解出x=f-1(y);
(2)将x,y互换得y =f-1(x);
(3)写出反函数的定义域(可根据原函数的定义域或反函数的解析式确定);
另外:分段函数的反函数可以分别求出各段函数的反函数再合成。
与“已知f(x)=ax+b(a>0且a≠1,b为常数)的图象经过点(1,1)...”考查相似的试题有:
- 下列各式:①; ②;③; ④.其中正确的有( )A.1个B.2个C.3个D.4个
- 函数f(x)=lg(x2-x-2)的定义域为集合A,函数g(x)=1-x的定义域为集合B.(1)求A∩B,A∪B;(2)若C={x|4x+p<0},C⊆A,求实...
- 抽气机每次抽出容器内空气的60%,要使容器内的空气少于原来的0.1%,则至少要抽( )(已知lg20.3010)A.6次B.7次C.8次D...
- 设函数f(x)=log2(10-ax),a为常数,若f(3)=2。(1)求a的值;(2)求使f(x)≤0的x的取值范围;(3)若在区间[1,3]内的每一...
- 函数f(x)=log12(x-4)的定义域是______.
- (文科学生做)不等式lg(-x)<x+1的解集是______.
- 已知直线x=2及x=4与函数图象的交点分别为A、B,与函数的交点分别为C、D,则直线AB与CD( )A.平行 B.相交且交点在第二象限 ...
- 已知函数的定义域为为正整数),值域为[0,2],则满足条件的整数对(m,n)共有 ( )A.1个B.7个C.8个D.16个
- 函数的反函数图象经过Q点,则Q点的一个坐标是 ( )A.(1,2)B.(3,1)C.(4,2)D.(5,2)
- 对于下列命题:①已知集合A={正四棱柱},B={长方体},则A∩B=B;②函数y=1lgx在(0,+∞)为单调函数;③在平面直角坐标系内,点M...