本试题 “已知△ABC的三个内角分别为A，B，C，向量m=(sinB，1-cosB)与向量n=(2，0)夹角的余弦角为12．（1）求角B的大小；（2）求sinA+sinC的取值范围．” 主要考查您对用数量积表示两个向量的夹角
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 用数量积表示两个向量的夹角
用数量积表示两个向量的夹角：
设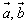
都是非零向量，
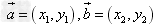，θ是
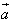与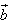
的夹角，根据向量数量积的定义及坐标表示可得
。
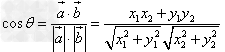向量数量积问题中方法提炼：
（1）平面向量的数量积的运算有两种形式，一是依据定义来计算，二是利用坐标来计算，具体应用哪种形式应根据已知条件的特征来选择；
（2）平面向量数量积的计算类似于多项式的运算，解题中要注意多项式运算方法的运用；
（3）平面向量数量积的计算中要注意平面向量基本定理的应用，选择合适的基底，以简化运算
（4）向量的数量积是一个数而不是一个向量。
发现相似题
与“已知△ABC的三个内角分别为A，B，C，向量m=(sinB，1-cosB)与向...”考查相似的试题有：
- 向量a、b满足（a-b）（2a+b）=-4，且|a|=2，|b|=4，则a与b夹角的余弦值等于（ ）。
- 设O为坐标原点，点M（2，1），点N（x，y）满足，则cos∠MON的最大值为[ ]A.B.C.D.
- 已知单位向量α，β，满足（α+2β）（2α-β）=1，则α与β夹角的余弦值为[ ]A.B.C.D.
- 如图，在△OAB中，已知P为线段AB上的一点，OP=x•OA+y•OB．（1）若BP=PA，求x，y的值；（2）若BP=3PA，|OA|=4，|OB|=2，且OA与O...
- 已知向量a=（cosα，sinα），b=（cosβ，sinβ），且a≠±b，那么a+b与a-b的夹角的大小是______．
- 设向量，均为单位向量，且|+|=1，则与夹角为[ ]A．B．C．D．
- 设两个非零向量a，b满足|a+b|=|a-b|=2|a|，则向量a+b与a-b的夹角是______．
- 已知a、b均为单位向量，（2a+b）•（a-2b）=-332，a与b的夹角为（ ）A．30°B．45°C．135°D．150°
- B1照样子，写出数量关系．例：实际比计划增产110．数量关系：计划产量+计划产量×110=实际产量，或者计划产量×（1+110）=实际...
- 若非零向量，满足||=||=|﹣|，则与+的夹角为（ ）。