本试题 “设函数f(x)=-32sin2x+12,A、B、C为△ABC的三个内角,若cosB=13,f(C2)=-14,且C为锐角,则sinA=______.” 主要考查您对正弦、余弦函数的图象与性质(定义域、值域、单调性、奇偶性等)
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 正弦、余弦函数的图象与性质(定义域、值域、单调性、奇偶性等)
正弦函数和余弦函数的图象:正弦函数y=sinx(x∈R)和余弦函数y=cosx(x∈R)的图象分别叫做正弦曲线和余弦曲线,
1.正弦函数 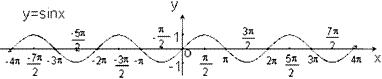
2.余弦函数
函数图像的性质
正弦、余弦函数图象的性质: 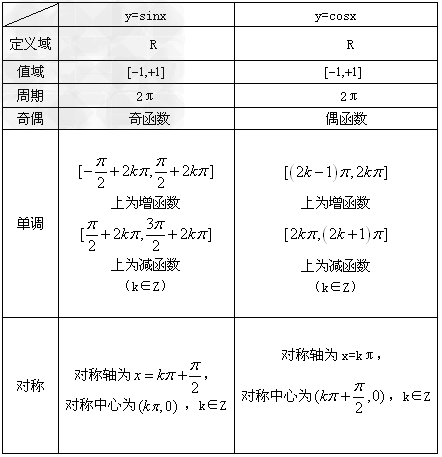
由上表知,正弦与余弦函数的定义域都是R,值域都是[-1,1],对y=sinx,当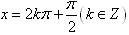 时,y取最大值1,
时,y取最大值1,
当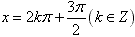 时,y取最小值-1;对y=cosx,当x=2kπ(k∈Z)时,y取最大值1,当x=2kπ+π(k∈Z)时,y取最小值-1。
时,y取最小值-1;对y=cosx,当x=2kπ(k∈Z)时,y取最大值1,当x=2kπ+π(k∈Z)时,y取最小值-1。
正弦、余弦函数图象的性质:

由上表知,正弦与余弦函数的定义域都是R,值域都是[-1,1],对y=sinx,当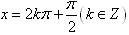 时,y取最大值1,
时,y取最大值1,
当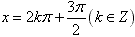 时,y取最小值-1;对y=cosx,当x=2kπ(k∈Z)时,y取最大值1,当x=2kπ+π(k∈Z)时,y取最小值-1。
时,y取最小值-1;对y=cosx,当x=2kπ(k∈Z)时,y取最大值1,当x=2kπ+π(k∈Z)时,y取最小值-1。
发现相似题
与“设函数f(x)=-32sin2x+12,A、B、C为△ABC的三个内角,若cosB=1...”考查相似的试题有:
- 如果函数f(x)在区间D上是凸函数,那么对于区间D内的任意x1,x2,…,xn,都有f(x1)+f(x2)+…+f(xn)n≤f(x1+x2+…+xnn).若y=s...
- 是否存在实数a,使得函数y=sin2x+a·cos x+a-在闭区间上的最大值是1?若存在,求出对应的a值;若不存在,试说明理由
- 下面有四个命题:(1)函数y=sin(23x+π2)是偶函数;(2)函数f(x)=|2cos2x-1|的最小正周期是π;(3)函数f(x)=sin(x+π4)在[...
- 已知简谐运动的部分图象如图示,则该简谐运动的最小正周期和初相分别为A.B.C.D.
- 的值域为___________。
- 函数的值域是 。
- 函数y=sin2x+sinx-1的值域为[ ]A.[-1,1]B.C.D.
- 函数y=2sin(x-π3)(0≤x≤π)的最大值与最小值之和为( )A.0B.2-3C.-1D.-l-3
- 若函数的最小正周期为1,则它的图像的一个对称中心为 ( )20070316 A.(-,0)B.(0,0)C.(-,0)D.(,0)
- 设的内角所对的边长分别为,且,A=,.(1)求函数的单调递增区间及最大值;(2)求的面积的大小