本试题 “如图,在直角坐标系xOy中,点P(1,)到抛物线C:=2px(P>0)的准线的距离为。点M(t,1)是C上的定点,A,B是C上的两动点,且线段AB被直线OM平分。(1)求p...” 主要考查您对函数的最值与导数的关系
点到直线的距离
直线与抛物线的应用
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 函数的最值与导数的关系
- 点到直线的距离
- 直线与抛物线的应用
函数的最大值和最小值:
在闭区间[a,b]上连续的函数f(x)在[a,b]上必有最大值与最小值,分别对应该区间上的函数值的最大值和最小值。
利用导数求函数的最值步骤:
(1)求f(x)在(a,b)内的极值;
(2)将f(x)的各极值与f(a)、f(b)比较得出函数f(x)在[a,b]上的最值。
用导数的方法求最值特别提醒:
①求函数的最大值和最小值需先确定函数的极大值和极小值,因此,函数极大值和极小值的判别是关键,极值与最值的关系:极大(小)值不一定是最大(小)值,最大(小)值也不一定是极大(小)值;
②如果仅仅是求最值,还可将上面的办法化简,因为函数fx在[a,b]内的全部极值,只能在f(x)的导数为零的点或导数不存在的点取得(下称这两种点为可疑点),所以只需要将这些可疑点求出来,然后算出f(x)在可疑点处的函数值,与区间端点处的函数值进行比较,就能求得最大值和最小值;
③当f(x)为连续函数且在[a,b]上单调时,其最大值、最小值在端点处取得。
生活中的优化问题:
生活中经常遇到求利润最大、用料最省、效率最高等问题,这些问题通常称为优化问题,解决优化问题的方法很多,如:判别式法,均值不等式法,线性规划及利用二次函数的性质等,
不少优化问题可以化为求函数最值问题.导数方法是解这类问题的有效工具.
用导数解决生活中的优化问题应当注意的问题:
(1)在求实际问题的最大(小)值时,一定要考虑实际问题的意义,不符合实际意义的值应舍去;
(2)在实际问题中,有时会遇到函数在区间内只有一个点使f'(x)=0的情形.如果函数在这点有极大(小)值,那么不与端点比较,也可以知道这就是最大(小)值;
(3)在解决实际优化问题时,不仅要注意将问题中涉及的变量关系用函数关系表示,还应确定出函数关系式中自变量的定义区间.
利用导数解决生活中的优化问题:
(1)运用导数解决实际问题,关键是要建立恰当的数学模型(函数关系、方程或不等式),运用导数的知识与方法去解决,主要是转化为求最值问题,最后反馈到实际问题之中.
(2)利用导数求f(x)在闭区间[a,b]上的最大值和最小值的步骤,
①求函数y =f(x)在(a,b)上的极值;
②将函数y=f(x)的各极值与端点处的函数值f(a)、f(b)比较,其中最大的一个是最大值,最小的一个是最小值.
(3)定义在开区间(a,b)上的可导函数,如果只有一个极值点,该极值点必为最值点.
点到直线的距离公式:
1、若点P(x0,y0)在直线Ax+By+C=0(A,B不同时为0)上,则Ax0+By0+C=0。
2、若点P(x0,y0)不在直线Ax+By+C=0(A,B不同时为0)上,则Ax0+By0+C≠0,此时点P(x0,y0)直线Ax+By+C=0(A,B不同时为0)的距离d= 。
。
点到直线的距离公式的理解:
①点到直线的距离是直线上的点与直线外一点的连线的最短距离(这是从运动观点来看的).
②若给出的直线方程不是一般式,则应先把方程化为一般式,再利用公式求距离.
③点到直线的距离公式适用于任何情况,其中点P在直线l上时,它到直线的距离为0.
④点到几种特殊直线的距离: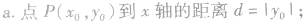
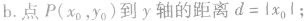
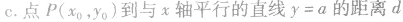

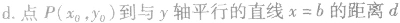
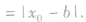
设直线l的方程为:Ax+By+C=0(A、B不同时为零),抛物线的方程为y2=2px(p>0),将直线的方程代入抛物线的方程,消去y(或x) 得到一元二次方程,进而应用根与系数的关系解题。
直线与抛物线的位置关系:
直线和抛物线的位置关系,可通过直线方程与抛物线方程组成的方程组的实数解的个数来确定,同时注意过焦点的弦的一些性质,如:
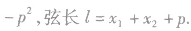
与“如图,在直角坐标系xOy中,点P(1,)到抛物线C:=2px(P>0...”考查相似的试题有:
- 已知函数,。(1)若,且函数存在单调递减区间,求的取值范围;(2)当时,求函数的取值范围。
- 已知函数f(x)=x|x2-a| (a∈R),(1)当a≤0时,求证函数f(x)在(-∞,+∞)上是增函数;(2)当a=3时,求函数f(x)在区间[0,b]上...
- 已知函数f(x)=ax3+bx2﹣3x(a,b∈R)在点(1,f(1))处的切线方程为y+2=0.(1)求函数f(x)的解析式;(2)若对于区间[...
- 若函数在区间[1,e]上的最小值为,则实数a的值为[ ]A.B.C.D.非上述答案
- 设函数(Ⅰ)若,函数是否有极值,若有则求出极值,若没有,请说明理由.(Ⅱ)若在其定义域内为单调函数,求实数p的取值范围.
- 已知函数。(Ⅰ)求f(x)的单调区间;(Ⅱ)若对于任意的x∈(0,+∞),都有f(x)≤,求k的取值范围。
- 已知函数f(x)=-alnx++x(a≠0),(1)若曲线y=f(x)在点(1,f(1))处的切线与直线x-2y=0垂直,求实数a的值;(2)讨论函数f(x)...
- 圆与直线相交于两点,圆心为,若,则的值为( )A.8B.C.D.3
- 设A(x1,y1),B(x2,y2)是平面直角坐标系xOy上的两点,现定义由点A到点B的一种折线距离ρ(A,B)为ρ(A,B)=|x2-x1|+|y2...
- 已知曲线C上任意一点M到点F(0,1)的距离比它到直线l:y=﹣2的距离小1.(1)求曲线C的方程;(2)过点P(2,2)的直线m与曲...