返回

高中数学

首页
首页 高中数学知识 集合间的基本关系 函数的单调性、最值 试题正文
  • 解答题
    定义在[-1，1]上的奇函数f（x）满足f（1）=1，且当a、b∈[-1，1]，a+b≠0时，有
    f(a)+f(b)
    a+b
    ＞0    ．
    （1）证明：f（x）是[-1，1]上的增函数；
    （2）若f（x）≤m2+2am+1对所有的x∈[-1，1]，a∈[-1，1]恒成立，求m的取值范围．
    本题信息：数学解答题难度较难 来源:未知
  • 本题答案
    查看答案
本试题 “定义在[-1，1]上的奇函数f（x）满足f（1）=1，且当a、b∈[-1，1]，a+b≠0时，有f(a)+f(b)a+b＞0．（1）证明：f（x）是[-1，1]上的增函数；（2）若f（x）≤m2+2am...” 主要考查您对

集合间的基本关系

函数的单调性、最值

等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
  • 集合间的基本关系
  • 函数的单调性、最值

集合与集合的关系有“包含”与“不包含”，“相等”三种：

 1、 子集概念：
一般地，对于两个集合A与B，如果集合A的任何一个元素都是集合B的元素，就说集合B包含A，记作A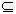B（或说A包含于B），
也可记为B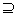A（B包含A），此时说A是B的子集；A不是B的子集，记作A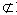B，读作A不包含于B

2、集合相等：
对于集合A和B，如果集合A中的每一个元素都是集合B的元素，反过来，集合B的每一个元素也都是集合A的元素，即集合A是集合B的子集，且集合B是集合A的子集，我么就说集合A和集合B相等，记作A=B

3、真子集：
对于集合A与B，如果A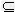B并且A≠B，则集合A是集合B的真子集，记作AB（B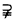A），读作A真包含于B（B真包含A） 


集合间基本关系：

性质1：

（1）空集是任何集合的子集，即A；

（2）空集是任何非空集合的真子集；

（3）传递性：AB，BCAC；AB，BCAC；

（4）AB，BAA=B。

性质2：

 子集个数的运算：含n个元素的集合A的子集有2n个，非空子集有2n-1个，非空真子集有2n-2个。


集合间基本关系性质：

（1）空集是任何集合的子集，即A；
（2）空集是任何非空集合的真子集；
（3）传递性：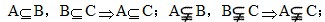 
（4）集合相等： 
（5）含n个元素的集合A的子集有2n个，非空子集有2n-1个，非空真子集有2n-2个。


单调性的定义：

1、对于给定区间D上的函数f（x），若对于任意x1，x2∈D，当x1＜x2时，都有f（x1）＜f（x2），则称f（x）是区间上的增函数；当x1＜x2时，都有f（x1）＞f（x2），则称f（x）是区间D上的减函数。

2、如果函数y=f（x）在区间上是增函数或减函数，就说函数y=f（x）在区间D上具有（严格的）单调性，区间D称为函数f（x）的单调区间。如果函数y=f（x）在区间D上是增函数或减函数，区间D称为函数f（x）的单调增或减区间 
 
3、最值的定义：
最大值：一般地，设函数y＝f（x）的定义域为I，如果存在实数M，满足： ①对于任意的x∈I，都有f（x）≤M；②存在x0∈I，使得f（x0）＝M；那么，称M是f（x）的最大值．
最小值：一般地，设函数y＝f（x）的定义域为I，如果存在实数M，满足： ①对于任意的x∈I，都有f（x）≥M；②存在x0∈I，使得f（x0）＝M；那么，称M是f（x）的最小值


判断函数f（x）在区间D上的单调性的方法：

（1）定义法：其步骤是：
①任取x1，x2∈D，且x1＜x2；
②作差f（x1）-f（x2）或作商 ，并变形；
③判定f（x1）-f（x2）的符号，或比较 与1的大小；
④根据定义作出结论。
（2）复合法：利用基本函数的单调性的复合。
（3）图象法：即观察函数在区间D上部分的图象从左往右看是上升的还是下降的。


发现相似题
与“定义在[-1，1]上的奇函数f（x）满足f（1）=1，且当a、b∈[-1，...”考查相似的试题有：