本试题 “设椭圆C1：=1（a＞b＞0）的左、右焦点分别为为，恰是抛物线C2：的焦点，点M为C1与C2在第一象限的交点，且｜MF2｜=．（1）求C1的方程；（2）平面上的点N满足，...” 主要考查您对椭圆的定义
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 椭圆的定义
椭圆的第一定义：
平面内与两个定点为F1，F2的距离的和等于常数（大于
）的轨迹叫做椭圆，这两个定点叫做椭圆的焦点，两焦点的距离叫做椭圆的焦距。特别地，当常数等于时，轨迹是线段F1F2，当常数小于时，无轨迹。
椭圆的第二定义：
平面内到定点F的距离和到定直线l的距离之比等于常数e（0＜e＜1）的点的轨迹，叫做椭圆，定点F叫椭圆的焦点，定直线l叫做椭圆的准线，e叫椭圆的离心率。
椭圆的定义应该包含几个要素：
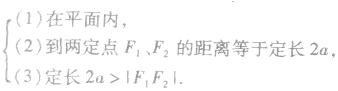
利用椭圆的定义解题：
当题目中出现一点在椭圆上的条件时，注意使用定义
发现相似题
与“设椭圆C1：=1（a＞b＞0）的左、右焦点分别为为，恰是抛物线C2...”考查相似的试题有：
- 平面内有一长度为2的线段AB和一动点P满足|PA|+|PB|=6，则|PA|的取值范围是（ ）A．[1，4]B．[1，6]C．[2，6]D．[2，4]
- 已知椭圆的离心率为，直线:与以原点为圆心、以椭圆的短半轴长为半径的圆相切.（1）求椭圆的方程；（2）设椭圆的左焦点为，右...
- （本题满分15分）设椭圆，已知(Ⅰ) 求椭圆E的方程；（Ⅱ）已知过点M(1,0)的直线交椭圆E于C,D两点，若存在动点N，使得直线NC,NM,...
- 求椭圆25x2+y2=25的长轴和短轴的长、焦点和顶点坐标及离心率.
- 正四面体P-ABC中，点M在面PBC内，且点M到点P的距离等于点M到底面ABC的距离则动点M在面PBC的轨迹是（ ）A．抛物线的一部分B．...
- 在平面直角坐标系中，已知焦距为4的椭圆的左、右顶点分别为，椭圆的右焦点为，过作一条垂直于轴的直线与椭圆相交于，若线段的...
- 椭圆的焦点在轴上，长轴长是短轴长的两倍，则的值为（ ）A．4B．2C．D．
- 椭圆上一点M到直线x+2y-10=0的距离的最小值为( )A．2B．C．2D．1
- 在平面直角坐标系xOy中，已知椭圆的左焦点为F，直线x－y－1＝0，x－y＋1＝0与椭圆分别相交于点A，B，C，D，则AF＋BF＋CF＋DF...
- 设F1，F2分别是椭圆＋y2＝1的左、右焦点，P是第一象限内该椭圆上的一点，且PF1⊥PF2，则点P的横坐标为( )A．1B．C．2D．