本试题 “已知向量a与b满足:|a|=4,|b|=3,(2a+3b)•(2a-b)=61.(Ⅰ)求a•b的值;(Ⅱ)求向量a与b的夹角;(Ⅲ)求|a-b|的值.” 主要考查您对用数量积表示两个向量的夹角
向量数量积的运算
向量模的计算
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 用数量积表示两个向量的夹角
- 向量数量积的运算
- 向量模的计算
用数量积表示两个向量的夹角:
设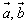 都是非零向量,
都是非零向量,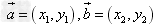 ,θ是
,θ是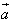 与
与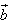 的夹角,根据向量数量积的定义及坐标表示可得
的夹角,根据向量数量积的定义及坐标表示可得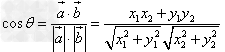 。
。
向量数量积问题中方法提炼:
(1)平面向量的数量积的运算有两种形式,一是依据定义来计算,二是利用坐标来计算,具体应用哪种形式应根据已知条件的特征来选择;
(2)平面向量数量积的计算类似于多项式的运算,解题中要注意多项式运算方法的运用;
(3)平面向量数量积的计算中要注意平面向量基本定理的应用,选择合适的基底,以简化运算
(4)向量的数量积是一个数而不是一个向量。
两个向量数量积的含义:
如果两个非零向量 ,
, ,它们的夹角为
,它们的夹角为 ,我们把数量
,我们把数量 叫做
叫做 与
与 的数量积(或内积或点积),记作:
的数量积(或内积或点积),记作: ,即
,即 。
。 叫
叫 在
在 上的投影。
上的投影。
规定:零向量与任一向量的数量积是0,注意数量积是一个实数,不再是一个向量。
数量积的的运算律:
已知向量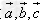 和实数λ,下面(1)(2)(3)分别叫做交换律,数乘结合律,分配律。
和实数λ,下面(1)(2)(3)分别叫做交换律,数乘结合律,分配律。
(1)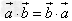 ;
;
(2)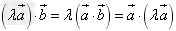 ;
;
(3)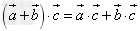 。
。
向量数量积的性质:
设两个非零向量
(1) ;
;
(2) ;
;
(3) ;
;
(4) ;
;
(5)当 ,
, 同向时,
同向时, ;当
;当 与
与 反向时,
反向时, ;当
;当 为锐角时,
为锐角时, 为正且
为正且 ,
, 不同向,
不同向, ;当
;当 为钝角时,
为钝角时, 为负且
为负且 ,
, 不反向,
不反向, 。
。
向量的模:
设 ,则有向线段
,则有向线段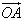 的长度叫做向量
的长度叫做向量 的长度或模,记作:
的长度或模,记作: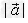 ,则
,则  。
。
向量模的坐标表示:
(1)若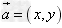 ,则
,则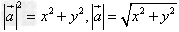 ;
;
(2)若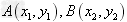 ,那么
,那么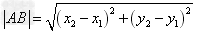 。
。
求向量的模:
求向量的模主要是利用公式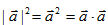 来解。
来解。
发现相似题
与“已知向量a与b满足:|a|=4,|b|=3,(2a+3b)•(2a-b)=61.(...”考查相似的试题有:
- 空间三点A(0,1,0),B(2,2,0),C(-1,3,1),则( ) A.与是共线向量 B.的单位向量是(1,1,0) C.与夹角的余弦...
- 设向量,满足:||=1,||=2,(+)=0,则与的夹角是[ ]A.30°B.60°C.90°D.120°
- 已知向量a、b的夹角为60°,且|a|=3,|b|=4,则(a+2b)•(a-b)=______.
- 设a= (x2 , -y2),b= (x2 , -y2),P(x,y)是曲线C上任意一点,且满足a•b=1.O为坐标原点,直线l:x-y-1=0与曲线C交于不同...
- 设a=(3sinx,cosx) , b=(cosx,-cosx),定义f(x)=a•b.(Ⅰ)求函数f(x)的周期;(Ⅱ)当x∈[0,π2]时,求函数f(x)的值域.
- 已知函数f(x)=3sinωx+cos(ωx+π3)+cos(ωx-π3)-1(ω>0,x∈R),且函数f(x)的最小正周期为π(1)求函数f(x)的解析式;(2)在...
- 已知向量a=(sinx,cosx),b=(cosx,-2cosx),-π4<x<π2.(Ⅰ)若a∥b,求x;(Ⅱ)设f(x)=a•b,求f(x)的单调减区间;...
- 已知在△OAB(O为原点)中,OA=(2cosa,2sina),OB=(5cosb,5sinb),若OA•OB=-5,则S△AOB的值为______.
- ______称为向量的长度(或称为模),记作 ______,______称为零向量,记作 ______,______称为单位向量.
- 已知,且,(1)求||,||;(2)若与的夹角为θ,求cosθ的值.