本试题 “在△ABC中,设∠A,∠B,∠C的对边分别为a,b,c,已知3cosA-2sin2A=0,(1)求∠A的大小;(2)若a=3,b+c=3(b>c),求b,c的值.” 主要考查您对同角三角函数的基本关系式
余弦定理
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 同角三角函数的基本关系式
- 余弦定理
同角三角函数的关系式:
(1)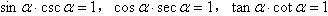 ;
;
(2)商数关系: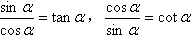 ;
;
(3)平方关系: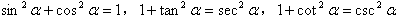 。
。
同角三角函数的基本关系的应用:
已知一个角的一种三角函数值,根据角的终边的位置利用同角三角函数的基本关系,可以求出这个角的其他三角函数值.
同角三角函数的基本关系的理解:
(1)在公式中,要求是同一个角,如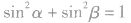 不一定成立.
不一定成立.
(2)上面的关系式都是对使它的两边具有意义的那些角而言的,如:基本三角关系式 。对一切α∈R成立;
。对一切α∈R成立;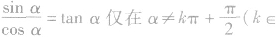 Z)时成立.
Z)时成立.
(3)同角三角函数的基本关系的应用极为为广泛,它们还有如下等价形式: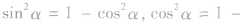

(4)在应用平方关系时,常用到平方根、算术平方根和绝对值的概念,应注意“±”的选取.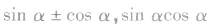 间的基本变形 三者通过
间的基本变形 三者通过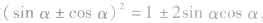 ,可知一求二,有关
,可知一求二,有关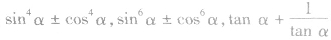 等化简都与此基本变形有广泛的联系,要熟练掌握。
等化简都与此基本变形有广泛的联系,要熟练掌握。
余弦定理:
三角形任意一边的平方等于其他两边的平方的和减去这两边与它们夹角的余弦的积的两倍,
即 。
。
推论:
在△ABC中,若a2+b2=c2,则C为直角;若a2+b2>c2,则C为锐角;若a2+b2<c2,则C为钝角。
余弦定理在解三角形中的应用:
(1)已知两边和夹角,
(2)已知三边。
其它公式:
射影公式: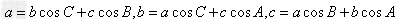
发现相似题
与“在△ABC中,设∠A,∠B,∠C的对边分别为a,b,c,已知3cosA-2sin...”考查相似的试题有:
- 若tanθ=2,则cos2θ=( )A.45B.-45C.35D.-35
- 函数,的图像与直线有且仅有两个不同的交点,则的取值范围是( )A.B.C.D.
- 已知,则=( )A.B.C.D.
- 已知-π2<α<0,sinα+cosα=-15,sinα-cosα的值是______.
- 已知sinα=22,则cos(π-2α)=______.
- 若cosα=-23,则tan2α-1=______.
- △ABC中,a,b,c分别是内角A,B,C的对边,且cos2B+3cos(A+C)+2=0,b=,则c:sinC=[ ]A.3:1B.:1C.:1D.2:1
- 如图所示,△ACD是边长为1的等边三角形,△ABC是等腰直角三角形,∠ACB=90°,BD交AC于点E.(1)求BD2的值;(2)求线段AE的长.
- △ABC中,a、b、c分别是角A、B、C的对边,若a2-c2=2b,且sinB=6cosA•sinC,则b的值为______.
- 锐角三角形ABC中,若A=2B,A,B,C所对的边分别为a,b,c.则下列四个结论:①sin3B=sin2C②tan3B2tanC2=1③π6<B<π4④ab∈(2,3]...