本试题 “已知函数的定义域为集合A,B={x|x<a},(1)若AB,求a的取值范围;(2)若全集U={x|x≤4},a=-1,求CUA及A∩(CUB)。” 主要考查您对集合间的基本关系
集合间交、并、补的运算(用Venn图表示)
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 集合间的基本关系
- 集合间交、并、补的运算(用Venn图表示)
集合与集合的关系有“包含”与“不包含”,“相等”三种:
1、 子集概念:
一般地,对于两个集合A与B,如果集合A的任何一个元素都是集合B的元素,就说集合B包含A,记作A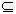 B(或说A包含于B),
B(或说A包含于B),
也可记为B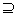 A(B包含A),此时说A是B的子集;A不是B的子集,记作A
A(B包含A),此时说A是B的子集;A不是B的子集,记作A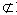 B,读作A不包含于B
B,读作A不包含于B
2、集合相等:
对于集合A和B,如果集合A中的每一个元素都是集合B的元素,反过来,集合B的每一个元素也都是集合A的元素,即集合A是集合B的子集,且集合B是集合A的子集,我么就说集合A和集合B相等,记作A=B
3、真子集:
对于集合A与B,如果A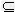 B并且A≠B,则集合A是集合B的真子集,记作A
B并且A≠B,则集合A是集合B的真子集,记作A B(B
B(B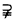 A),读作A真包含于B(B真包含A)
A),读作A真包含于B(B真包含A)
集合间基本关系:
性质1:
(1)空集是任何集合的子集,即A;
(2)空集是任何非空集合的真子集;
(3)传递性:AB,BCAC;AB,BCAC;
(4)AB,BAA=B。
性质2:
子集个数的运算:含n个元素的集合A的子集有2n个,非空子集有2n-1个,非空真子集有2n-2个。
集合间基本关系性质:
(1)空集是任何集合的子集,即A;
(2)空集是任何非空集合的真子集;
(3)传递性: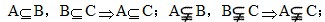
(4)集合相等:
(5)含n个元素的集合A的子集有2n个,非空子集有2n-1个,非空真子集有2n-2个。
1、交集概念:
(1)一般地,由所有属于集合A且集合B的元素所组成的集合,叫做A与B的交集,记作A∩B,读作A交B,表达式为A∩B={x|x∈A且x∈B}。
(2)韦恩图表示为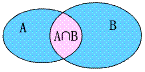 。
。
2、并集概念:
(1)一般地,由所有属于集合A或集合B的元素所组成的集合,叫做A与B的并集,记作A∪B,读作A并B,表达式为A∪B={x|x∈A或x∈B}。
(2)韦恩图表示为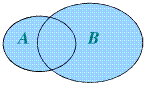 。
。
3、全集、补集概念:
(1)全集:一般地,如果一个集合含有我们所要研究的各个集合的全部元素,就称这个集合为全集,通常记作U。
补集:对于一个集合A,由全集U中所有不属于A的元素组成的集合称为集合A相对于全集U的补集,记作CUA,读作U中A的补集,表达式为CUA={x|x∈U,且x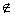 A}。
A}。
(2)韦恩图表示为 。
。
1、交集的性质:
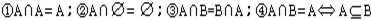
2、并集的性质:
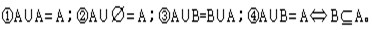
3、补集的性质:
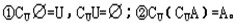
与“已知函数的定义域为集合A,B={x|x<a},(1)若AB,求a的取值...”考查相似的试题有:
- 设全集为R, 函数的定义域为M, 则为 ( )A.[-1,1]B.(-1,1)C.D.
- 函数f(x)=lg(x2﹣2x﹣3)的定义域是集合M,函数的定义域是集合P,则P∪M等于[ ]A.(﹣∞,﹣1)∪[1,+∞)B.(﹣∞,﹣3)∪[...
- 已知全集U={a,b,c,d,e},A={c,d,e},B={a,b,e},则集合(∁UA)∩B=______.
- 设集合,则 ( )A.B.C.D.
- 设集合M={-1,0,1},N={a,a2},则使M∩N=N成立的实数a的值是______.
- 设集合,,则等于( )A.{2} B.{1,2,4,6}C.{1,2,4}D.{2,6}
- 已知全集U={1,2,3,4,5,6},集合M={2,3,5},N={4,5},则CU(M∪N)等于[ ]A.{1,3,5}B.{2,4,6}C.{1,5}D.{1,6}
- 集合,则 .
- 设集合,则A.B.C.2D.-2
- 、,,若,则的取值范围是 ▲ .