本试题 “已知中心在原点的双曲线C的右焦点为(2,0),实轴长为2。(1)求双曲线C的方程;(2)若直线l:y=kx+与双曲线C左支交于A、B两点,求k的取值范围;(3)在(2...” 主要考查您对线段的定比分点
直线的倾斜角与斜率
双曲线的标准方程及图象
直线与双曲线的应用
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 线段的定比分点
- 直线的倾斜角与斜率
- 双曲线的标准方程及图象
- 直线与双曲线的应用
线段的定比分点定义:
设点P是直线P1P2上异于P1、P2的任意一点,若存在一个实数λ,使P1P=λPP2,λ叫做点P分有向线段 所成的比,P点叫做有向线段
所成的比,P点叫做有向线段  的以定比为λ的定比分点。
的以定比为λ的定比分点。
当P点在线段 P1P2上时,λ>0;当P点在线段 P1P2的延长线上时,λ<-1;当P点在线段P2P1的延长线上时 -1<λ<0。
若点P分有向线段 所成的比为λ,则点P分有向线段
所成的比为λ,则点P分有向线段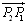 所成的比为
所成的比为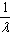 。
。
有向线段的定比分点的坐标公式:
(1)设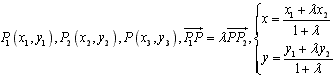 ,
,
在使用定比分点的坐标公式时,应明确(x,y),(x1,y1),(x2,y2)的意义,即分别为分点,起点,终点的坐标。一般在计算中应根据题设,自行确定起点,分点和终点并根据这些点确定对应的定比λ。
(2)当λ=1时,就得到P1P2的中点公式: ;
;
(3)三角形ABC的重心公式:设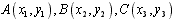 ,则重心
,则重心 。
。
直线的倾斜角的定义:
x轴正向与直线向上方向之间所成的角叫直线的倾斜角。特别地,当直线与x轴平行或重合时,我们规定它的倾斜角为0度。因此,倾斜角的取值范围是0°≤α<180°。
直线的斜率的定义:
倾斜角不是90°的直线,它的倾斜角的正切值叫做这条直线的斜率。直线的斜率常用k表示。即k=tanα。斜率反映直线与x轴的倾斜程度。
直线斜率的性质:
当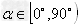 时,k≥0;当
时,k≥0;当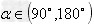 时,k<0;当
时,k<0;当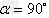 时,k不存在。
时,k不存在。
直线倾斜角的理解:
(1)注意“两个方向”:直线向上的方向、x轴的正方向;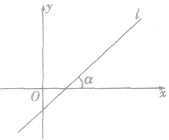
(2)规定当直线和x轴平行或重合时,它的倾斜角为0度。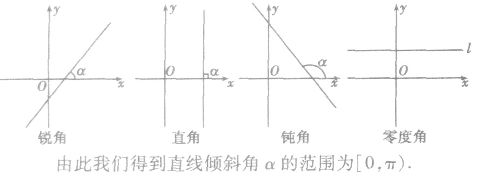
直线倾斜角的意义:
①直线的倾斜角,体现了直线对x轴正向的倾斜程度;
②在平面直角坐标系中,每一条直线都有一个确定的倾斜角;
③倾斜角相同,未必表示同一条直线。
直线斜率的理解:
每条直线都有倾斜角,但每条直线不一定都有斜率, 斜率不存在;当
斜率不存在;当 也逐渐增大;
也逐渐增大;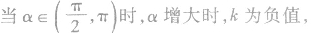 且逐渐增大。
且逐渐增大。
双曲线的标准方程:
(1)中心在原点,焦点在x轴上: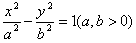 ;
;
(2)中心在原点,焦点在y轴上: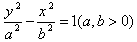 。
。
双曲线的图像:
(1)焦点在x轴上的双曲线的图像 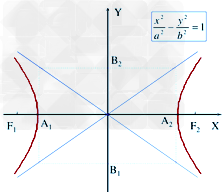 ;
;
(2)焦点在y轴上的双曲线的图像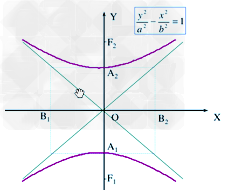 。
。
判断双曲线的焦点在哪个轴上:
判断双曲线的焦点在哪个轴上的方法看未知数前的系数,哪一个为正,焦点就在哪一个轴上.
定义法求双曲线的标准方程:
求动点的轨迹方程时,可利用定义先判断动点的轨迹,再写出方程.平面几何中的定理性质在解决解析几何问题时起着简化运算的作用,一定要注意应用,根据双曲线的定义,到两个定点的距离之差的绝对值是一个常数的点的轨迹是双曲线,可以求双曲线的标准方程,
待定系数法求双曲线的标准方程:
在求双曲线标准方程时,可先设出其标准方程,再根据双曲线的参数a,b,c,e的取值及相互之间的关系,求出a,b的值,已知双曲线的渐近线方程,求双曲线方程时,可利用共渐近线双曲线系方程 ,再由其他条件求λ.若焦点不确定时,要注意分类讨论.
,再由其他条件求λ.若焦点不确定时,要注意分类讨论.
利用双曲线的性质求解有关问题:
要解决双曲线中有关求离心率或求离心率范围的问题,应找好题中的等量关系或不等关系,构造出离心率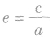 的关系式,这里应和椭圆中a,b,c的关系区分好,即
的关系式,这里应和椭圆中a,b,c的关系区分好,即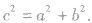
几种特殊的双曲线:
| 等轴双曲线 | 实轴和虚轴相等的双曲线叫做等轴双曲线.离心率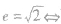 两条渐近线互相垂直 两条渐近线互相垂直 |
| 共轭双曲线 |
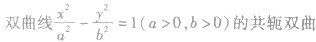
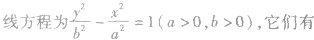

 |
| 共渐近线的双曲线 |

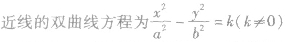 |
直线与双曲线:
设直线l的方程为:Ax+By+C=0(A、B不同时为零),双曲线的方程: ,将直线的方程代入双曲线的方程,消去y(或x)得到一元二次方程,进而应用根与系数的关系解题。
,将直线的方程代入双曲线的方程,消去y(或x)得到一元二次方程,进而应用根与系数的关系解题。
双曲线的综合问题:
双曲线知识通常与圆、椭圆、抛物线或数列、向量及不等式、三角函数相联系,综合考查数学知识及应用是高考的重点,应用中应注意对知识的综合及分析能力,双曲线的标准方程和几何性质中涉及很多基本量,如“a,b,c,e"树立基本量思想对于确定双曲线方程和认识其几何性质有很大帮助.另外,渐近线是双曲线特有的,双曲线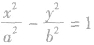 的渐近线方程可记为
的渐近线方程可记为
 为渐近线的双曲线方程可设为
为渐近线的双曲线方程可设为 .特别地,等轴双曲线方程可设为
.特别地,等轴双曲线方程可设为
 的垂直关系的证明可以通过
的垂直关系的证明可以通过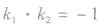 来证明,也可以通过
来证明,也可以通过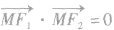 来证明,它体现了证明解析几何问题方法的多样性.
来证明,它体现了证明解析几何问题方法的多样性.与“已知中心在原点的双曲线C的右焦点为(2,0),实轴长为2。(1...”考查相似的试题有:
- 已知点M(6,2)和M2(1,7).直线y=mx-7与线段M1M2的交点M分有向线段M1M2的比为3:2,则m的值为( ) A.- B.- C. D.4
- 若直线l经过第二、四象限,则直线l的倾斜角范围是[ ]A.[0°,90°]B.[90°,180°]C.(90°,180°)D.[0°,180°)
- 已知直线l的斜率为2,且过点A(-1,-2),B(3,m),则m的值为( )A.6B.10C.2D.0
- 若直线xcosθ+ysinθ-1=0与圆(x-1)2+(y-sinθ)2=116相切,且θ为锐角,则这条直线的斜率是( )A.-33B.-3C.33D.3
- 点P在曲线y=x3-x+23上移动,设在点P处的切线的倾斜角为为α,则α的取值范围是______.
- 已知平面上一定点C(4,0)和一定直线l:x=1,P为该平面上一动点,作PQ⊥l,垂足为Q,且(PC+2PQ)•(PC-2PQ)=0.(1)问:点P在...
- △ABC中,B(-5,0),C(5,0),且SinC-SinB=45SinA,则点A的轨迹方程______.
- 已知双曲线的中心在原点,焦点为F1(0,-22),F2(0,22),且离心率e=324,求双曲线的标准方程.
- 在直角坐标系xOy中,设P为两动圆(x+2)2+y2=(r+2)2,(x-2)2+y2=r2(r>1)的一个交点,记动点P的轨迹为C.给出下列三个...
- 设圆C与两圆(x+)2+y2=4,(x-)2+y2=4中的一个内切,另一个外切。(1)求圆C的圆心轨迹L的方程;(2)已知点M(,),F(,...