已知集合A={sinnπ2|n∈N，N是自然数集}．（1）用列举法表示集合A；（2）任取p∈A，q∈A，记向量a=(1，p)，b=(q，1),高中,数学试题,集合的含义及表示考点,平面向量基本定理及坐标表示考点,好技网

解答题
已知集合A={sin
nπ
2
|n∈N，N是自然数集}．
（1）用列举法表示集合A；
（2）任取p∈A，q∈A，记向量
a
=(1，p)，
b
=(q，1)，求
a
∥
b
的概率．

本题信息：数学解答题难度较难来源:未知
本题答案
查看答案

本试题 “已知集合A={sinnπ2|n∈N，N是自然数集}．（1）用列举法表示集合A；（2）任取p∈A，q∈A，记向量a=(1，p)，b=(q，1)，求a∥b的概率．” 主要考查您对
集合的含义及表示

平面向量基本定理及坐标表示
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。

集合的含义及表示
平面向量基本定理及坐标表示

集合的概念：

1、集合：一般地我们把一些能够确定的不同对象的全体称为集合（简称集）；集合通常用大写的拉丁字母表示，如A、B、C、……。
元素：集合中每个对象叫做这个集合的元素，元素通常用小写的拉丁字母表示，如a、b、c、……
2、元素与集合的关系：
（1）属于：如果a是集合A的元素，就说a属于A，记作a∈A
（2）不属于：如果a不是集合A的元素，就说a不属于A，记作 3、集合分类根据集合所含元素个属不同，可把集合分为如下几类：
（1）把不含任何元素的集合叫做空集Ф
（2）含有有限个元素的集合叫做有限集
（3）含有无穷个元素的集合叫做无限集

常用数集及其表示方法：

（1）非负整数集（自然数集）：全体非负整数的集合.记作N
（2）正整数集：非负整数集内排除0的集.记作N*或N+
（3）整数集：全体整数的集合.记作Z
（4）有理数集：全体有理数的集合.记作Q
（5）实数集：全体实数的集合.记作R

集合中元素的特性：

（1）确定性：给定一个集合，任何对象是不是这个集合的元素是确定的了. 任何一个元素要么属于该集合，要么不属于该集合，二者必具其一。
（2）互异性：集合中的元素一定是不同的.
（3）无序性：集合中的元素没有固定的顺序.

易错点:
（1）自然数集包括数0.
（2）非负整数集内排除0的集.记作N*或N+，Q、Z、R等其它数集内排除0的集，也这样表示，例如，整数集内排除0的集，表示成Z

平面向量的基本定理：

如果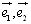是同一平面内的两个不共线的向量，那么对这一平面内的任一向量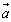存在唯一的一对有序实数使成立，不共线向量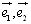表示这一平面内所有向量的一组基底。

平面向量的坐标运算：

在平面内建立直角坐标系，以与x轴、y轴方向相同的两个单位向量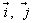为基底，则平面内的任一向量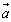可表示为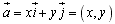，称（x，y）为向量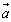的坐标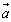，=（x，y）叫做向量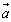的坐标表示。

基底在向量中的应用：

(l)用基底表示出相关向量来解决向量问题是常用的方法之一．
(2)在平面中选择基底主要有以下几个特点：①不共线；②有公共起点；③其长度及两两夹角已知．(3)用基底表示向量，就是利用向量的加法和减法对有关向量进行分解。

用已知向量表示未知向量：

用已知向量表示未知向量，一定要结合图像，可从以下角度如手：
（1）要用基向量意识，把有关向量尽量统一到基向量上来；
（2）把要表示的向量标在封闭的图形中，表示为其它向量的和或差的形式，进而寻找这些向量与基向量的关系；
（3）用基向量表示一个向量时，如果此向量的起点是从基底的公共点出发的，一般考虑用加法，否则用减法，如果此向量与一个易求向量共线，可用数乘。

发现相似题

与“已知集合A={sinnπ2|n∈N，N是自然数集}．（1）用列举法表示集...”考查相似的试题有：