本试题 “在三棱锥A-BCD中,侧棱AC、AC、AD两两垂直,△ABC、△ACD、△ADB 的面积分别为22、32、62,则该三棱锥外接球的表面积为( )A.2πB.46πC.6πD.24π” 主要考查您对球的表面积与体积
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 球的表面积与体积
球的体积公式:
V球=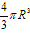 ;
;
球的表面积:
S球面=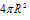
求球的表面积和体积的关键:
由球的表面积和体积公式可知,求球的表面积和体积的关键是求出半径。
常用结论:
1.若球的表面积变为原来的2倍,则半径变为原来的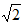 倍.
倍.
2.若球半径变为原来的2倍,则表面积变为原来的4倍.
3.若两球表面积之比为1:2,则其体积之比是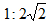 .
.
4.若两球体积之比是1:2,则其表面积之比是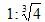 .
.
发现相似题
与“在三棱锥A-BCD中,侧棱AC、AC、AD两两垂直,△ABC、△ACD、△ADB...”考查相似的试题有:
- 圆柱的高等于球的直径,圆柱的侧面积等于球的表面积,设圆柱的体积为V,则球的体积为( )A.V3B.2V3C.3V2D.2V
- :在四面体ABCD中,设AB=1,CD=,直线AB与CD的距离为2,夹角为,则四面体ABCD的体积等于A. B. C. D.
- 如图所示,正四棱锥P-ABCD的底面积为3,体积为,E为侧棱PC的中点,则PA与BE所成的角为__________.
- 已知四面体的四个顶点都在球的球面上,若平面,,且,,则球的表面积为( )A.B.C.D.
- 周长为20cm的矩形,绕一边旋转成一个圆柱,则圆柱体积的最大值为 cm3
- 如图,在长方体ABCD-A1B1C1D1中,AB=AD=3cm,AA1=2cm,则四棱锥A-BB1D1D的体积为 cm3.
- 在球O的表面有A、B、C三个点,且∠ABC=∠BOC=∠COA=,△ABC的外接圆半径为2,那么这个球的表面积为[ ]A.48πB.36πC.24πD.12π
- 一个空间四边形的四条边及对角线的长均为,二面角的余弦值为,则下列论断正确的是 A.空间四边形的四个顶点在同一球面上且此...
- 已知球O的面上四点A、B、C、D,DA⊥平面ABC,AB⊥BC,DA=AB=BC=,则球O的表面积是( ) A.6π B.8π C.9π D.16π
- 已知三棱锥的三视图如图所示,则它的外接球的表面积为[ ]A.16πB.8πC.4πD.2π