本试题 “点P是曲线x2-y-2lnx=0上任意一点,则点P到直线4x+4y+1=0的最小距离是( )A.22(1-ln2)B.22(1+ln2)C.22(12+ln2)D.12(1+ln2)” 主要考查您对导数的运算
两直线平行、垂直的判定与性质
两条平行直线间的距离
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 导数的运算
- 两直线平行、垂直的判定与性质
- 两条平行直线间的距离
常见函数的导数:
(1)C′=0 ;(2)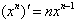 ;(3)
;(3)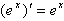 ;(4)
;(4) ;(5)
;(5)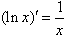 ;(6)
;(6)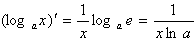 ;(7)
;(7)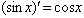 ;(8)
;(8)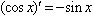
导数的四则运算:
(1)和差: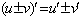
(2)积: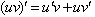
(3)商:
复合函数的导数:
运算法则复合函数导数的运算法则为: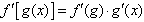
复合函数的求导的方法和步骤:
(1)分清复合函数的复合关系,选好中间变量;
(2)运用复合函数求导法则求复合函数的导数,注意分清每次是哪个变量对哪个变量求导数;
(3)根据基本函数的导数公式及导数的运算法则求出各函数的导数,并把中间变量换成自变量的函数。
求复合函数的导数一定要抓住“中间变量”这一关键环节,然后应用法则,由外向里一层层求导,注意不要漏层。
两直线平行、垂直的判定的文字表述:
平行判断的文字表述:如果两条不重合的直线(存在斜率)平行,则它们的斜率相等;反之,如果两条不重合直线的斜率相等,则它们平行;
垂直判断的文字表述:如果两条直线都有斜率,且它们互相垂直,那么它们斜率之积为-1;反之,如果两条直线的斜率之积为-1,那么它们互相垂直
两直线平行、垂直的判定的符号表示:
1、若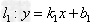 ,
,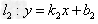
(1)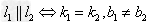 ;
;
(2)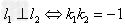 。
。
2、若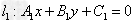 ,
,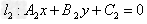 ,且A1、A2、B1、B2都不为零,
,且A1、A2、B1、B2都不为零,
(1)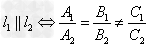 ;
;
(2)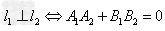 。
。
两直线平行的判断的理解:
 成立的前提条件是两条直线的斜率存在,分别为
成立的前提条件是两条直线的斜率存在,分别为
 当两条直线不重合且斜率均不存在时,
当两条直线不重合且斜率均不存在时,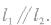
两直线垂直的判断的理解:
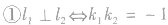 成立的前提条件是斜率都存在且不等于零.
成立的前提条件是斜率都存在且不等于零.
②两条直线中,一条斜率不存在,同时另一条斜率等于零,则两条直线垂直,这样,两条直线垂直的判定就可叙述为:一般地,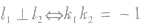 ,或一条直线的斜率不存在,同时另一条直线的斜率等于零。
,或一条直线的斜率不存在,同时另一条直线的斜率等于零。
求与已知直线垂直的直线方程的方法:
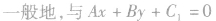 垂直的直线方程可设为
垂直的直线方程可设为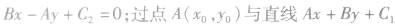
 垂直的直线方程可设为
垂直的直线方程可设为
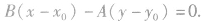
(2)利用互相垂直的直线之间的关系求出斜率,再用点斜式写出直线方程。
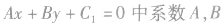 决定直线的斜率,因此,与直线
决定直线的斜率,因此,与直线
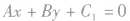 平行的直线方程可设为
平行的直线方程可设为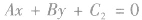 ,这是常常采用的解题技巧。
,这是常常采用的解题技巧。
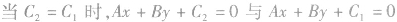 重合。
重合。(2)一般地,经过点

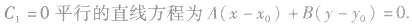
两条平行直线间的距离:
两平行线l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0间的距离为d=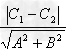 。
。
对两条平行直线间的距离公式的理解:
①两条平行直线间的距离,就是在其中一条直线上任取一点,这个点到另一条直线的距离,此点一般可以取直线上的特殊点,该方法体现了化归思想,即由线线间的距离到点线间的距离的转化,当然点线间的距离也可以化归为点点间的距离来求解;
②当利用两条平行直线间的距离公式d= 时,一定要先将两直线的方程化为一般形式且x和y的系数对应相等;
时,一定要先将两直线的方程化为一般形式且x和y的系数对应相等;
③如果两平行直线的方程用斜截式方程表示为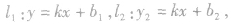 那么两平行直线间的距离公式为
那么两平行直线间的距离公式为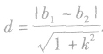
与“点P是曲线x2-y-2lnx=0上任意一点,则点P到直线4x+4y+1=0的最...”考查相似的试题有:
- 函数的导数为_____________________;
- 函数的导数 ,
- 已知f(x)=lnx+cosx,则f/(π2)=______.
- A.B.C.D.
- (2014·哈尔滨模拟)已知函数f(x)=x2+,g(x)=-m.若∀x1∈[1,2],∃x2∈[-1,1]使f(x1)≥g(x2),则实数m的取值范围是__________.
- 函数y=x+1x在x=1处的导数是______.
- 设向量a=(sinx,1),b=(1,cosx),记f(x)=a•b,f′(x)是f(x)的导函数.(I)求函数F(x)=f(x)f′(x)+f2(x)的最大值...
- 已知直线l1:(k-3)x+(5-k)y+1=0与l2:2(k-3)x-2y+3=0垂直,则K的值是( ) A.1或3 B.1或5 C.1或4 D.1或2
- 直线l1,l2的方程分别为y=3x-4,y=2x+1,则l1,l2的关系是[ ]A.垂直B.相交但不垂直C.重合D.以上都不对
- 已知双曲线C的中心是原点,右焦点为F(,0),一条渐近线m:x+y=0,设过点A(-3,0)的直线l的方向向量,(1) 求双曲线C的方...