本试题 “如图,设P是抛物线C1:x2=y上的动点.过点P做圆C2:x2+(y+3)2=1的两条切线,交直线l:y=-3于A,B两点。(1)求C2的圆心M到抛物线C1准线的距离;(2)是否存...” 主要考查您对导数的概念及其几何意义
点到直线的距离
圆的切线方程
抛物线的性质(顶点、范围、对称性、离心率)
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 导数的概念及其几何意义
- 点到直线的距离
- 圆的切线方程
- 抛物线的性质(顶点、范围、对称性、离心率)
平均变化率:
一般地,对于函数y =f(x),x1,x2是其定义域内不同的两点,那么函数的变化率可用式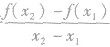 表示,我们把这个式子称为函数f(x)从x1到x2的平均变化率,习惯上用
表示,我们把这个式子称为函数f(x)从x1到x2的平均变化率,习惯上用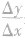 表示,即平均变化率
表示,即平均变化率
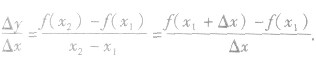
上式中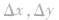 的值可正可负,但
的值可正可负,但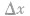 不为0.f(x)为常数函数时,
不为0.f(x)为常数函数时,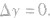
瞬时速度:
如果物体的运动规律是s=s(t),那么物体在时刻t的瞬时速度v就是物体在t到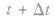 这段时间内,当
这段时间内,当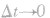 时平均速度的极限,即
时平均速度的极限,即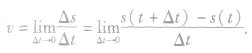
若物体的运动方程为s=f(t),那么物体在任意时刻t的瞬时速度v(t)就是平均速度v(t,d)为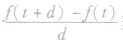 当d趋于0时的极限.
当d趋于0时的极限.
函数y=f(x)在x=x0处的导数的定义:
一般地,函数y=f(x)在x=x0处的瞬时变化率是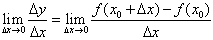 ,我们称它为函数y=f(x)在x=x0处的导数,记作
,我们称它为函数y=f(x)在x=x0处的导数,记作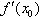 或
或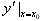 ,即
,即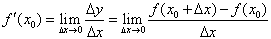 。
。
导函数:
如果函数y =f(x)在开区间(a,6)内的每一点都可导,则称在(a,b)内的值x为自变量,以x处的导数称为f(x为函数值的函数为fx)在(a,b)内的导函数,简称为f(x)在(a,b)内的导数,记作f′(x)或y′.即f′(x)=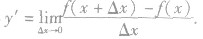
切线及导数的几何意义:
(1)切线:PPn为曲线f(x)的割线,当点Pn(xn,f(xn))(n∈N)沿曲线f(x)趋近于点P(x0,f(x0))时,割线PPn趋近于确定的位置,这个确定的位置的直线PT称为点P处的切线。
(2)导数的几何意义:函数f(x)在x=x0处的导数就是切线PT的斜率k,即k=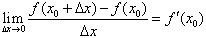 。
。
瞬时速度特别提醒:
①瞬时速度实质是平均速度当 时的极限值.
时的极限值.
②瞬时速度的计算必须先求出平均速度,再对平均速度取极限,
函数y=f(x)在x=x0处的导数特别提醒:
①当 时,比值
时,比值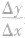 的极限存在,则f(x)在点x0处可导;若
的极限存在,则f(x)在点x0处可导;若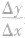 的极限不存在,则f(x)在点x0处不可导或无导数.
的极限不存在,则f(x)在点x0处不可导或无导数.
②自变量的增量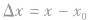 可以为正,也可以为负,还可以时正时负,但
可以为正,也可以为负,还可以时正时负,但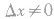 .而函数的增量
.而函数的增量 可正可负,也可以为0.
可正可负,也可以为0.
③在点x=x0处的导数的定义可变形为:

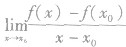
导函数的特点:
①导数的定义可变形为: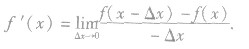
②可导的偶函数其导函数是奇函数,而可导的奇函数的导函数是偶函数,
③可导的周期函数其导函数仍为周期函数,
④并不是所有函数都有导函数.
⑤导函数 与原来的函数f(x)有相同的定义域(a,b),且导函数
与原来的函数f(x)有相同的定义域(a,b),且导函数 在x0处的函数值即为函数f(x)在点x0处的导数值.
在x0处的函数值即为函数f(x)在点x0处的导数值.
⑥区间一般指开区间,因为在其端点处不一定有增量(右端点无增量,左端点无减量).
导数的几何意义(即切线的斜率与方程)特别提醒:
①利用导数求曲线的切线方程.求出y=f(x)在x0处的导数f′(x);利用直线方程的点斜式写出切线方程为y-y0 =f′(x0)(x- x0).
②若函数在x= x0处可导,则图象在(x0,f(x0))处一定有切线,但若函数在x= x0处不可导,则图象在(x0,f(x0))处也可能有切线,即若曲线y =f(x)在点(x0,f(x0))处的导数不存在,但有切线,则切线与x轴垂直.
③注意区分曲线在P点处的切线和曲线过P点的切线,前者P点为切点;后者P点不一定为切点,P点可以是切点也可以不是,一般曲线的切线与曲线可以有两个以上的公共点,
④显然f′(x0)>0,切线与x轴正向的夹角为锐角;f′(x0)<o,切线与x轴正向的夹角为钝角;f(x0) =0,切线与x轴平行;f′(x0)不存在,切线与y轴平行.
点到直线的距离公式:
1、若点P(x0,y0)在直线Ax+By+C=0(A,B不同时为0)上,则Ax0+By0+C=0。
2、若点P(x0,y0)不在直线Ax+By+C=0(A,B不同时为0)上,则Ax0+By0+C≠0,此时点P(x0,y0)直线Ax+By+C=0(A,B不同时为0)的距离d= 。
。
点到直线的距离公式的理解:
①点到直线的距离是直线上的点与直线外一点的连线的最短距离(这是从运动观点来看的).
②若给出的直线方程不是一般式,则应先把方程化为一般式,再利用公式求距离.
③点到直线的距离公式适用于任何情况,其中点P在直线l上时,它到直线的距离为0.
④点到几种特殊直线的距离: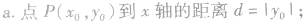
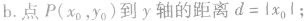
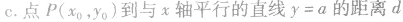

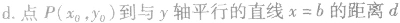
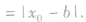
圆的切线方程:
1、已知圆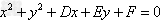 ,
,
(1)若已知切点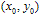 在圆上,则切线只有一条,其方程是
在圆上,则切线只有一条,其方程是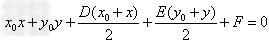 ;
;
(2)当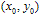 圆外时,
圆外时,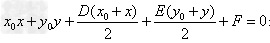 表示过两个切点的切点弦方程。
表示过两个切点的切点弦方程。
(3)过圆外一点的切线方程可设为 ,再利用相切条件求k,这时必有两条切线。
,再利用相切条件求k,这时必有两条切线。
(4)斜率为k的切线方程可设为y=kx+b,再利用相切条件求b,必有两条切线。
2、已知圆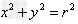 ,
,
(1)过圆上的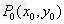 点的切线方程为
点的切线方程为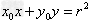 ;
;
(2)斜率为k的圆的切线方程为 。
。
圆的切线方程的求法:
①代数法:设出切线方程,利用切线与圆仅有一个交点,将直线方程代入圆的方程,从而△=0,可求解;
②几何法利用几何特征:圆心到切线的距离等于圆的半径,可求解.
过定点的圆的切线方程:
①过圆上一点的切线方程:
与圆 的切线方程是
的切线方程是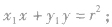
与圆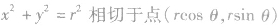 的切线方程是
的切线方程是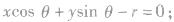
与圆 的切线方程是
的切线方程是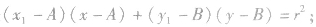
与圆 的切线方程是
的切线方程是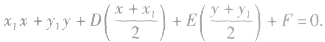
②过圆外一点的切线方程:设 外一点,求过P0点的圆的切线.
外一点,求过P0点的圆的切线.
方法l:设切点是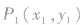 ,解方程组
,解方程组

方法2:设切线方程是
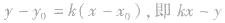
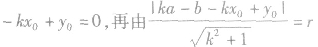 ,再由
,再由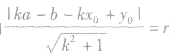 求出待定系数k,就可写出切线方程.
求出待定系数k,就可写出切线方程.特别提醒:一般说来,方法2比较简便,但应注意,可能遗漏k不存在的切线.因此,当解出的k值唯一时,应观察图形,看是否有垂直于x轴的切线.
抛物线的性质(见下表):

抛物线的焦点弦的性质:


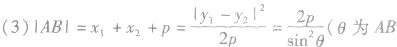



关于抛物线的几个重要结论:
(1)弦长公式同椭圆.
(2)对于抛物线y2=2px(p>0),我们有P(x0,y0)在抛物线内部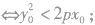 P(x0,y0)在抛物线外部
P(x0,y0)在抛物线外部
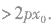
(3)抛物线y2=2px上的点P(x1,y1)的切线方程是 抛物线y2=2px(p>0)的斜率为k的切线方程是y=kx+
抛物线y2=2px(p>0)的斜率为k的切线方程是y=kx+
(4)抛物线y2=2px外一点P(x0,y0)的切点弦方程是
(5)过抛物线y2=2px上两点
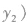 的两条切线交于点M(x0,y0),则
的两条切线交于点M(x0,y0),则
(6)自抛物线外一点P作两条切线,切点为A,B,若焦点为F,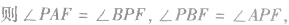 又若切线PA⊥PB,则AB必过抛物线焦点F.
又若切线PA⊥PB,则AB必过抛物线焦点F.
利用抛物线的几何性质解题的方法:
根据抛物线定义得出抛物线一个非常重要的几何性质:抛物线上的点到焦点的距离等于到准线的距离.利用抛物线的几何性质,可以进行求值、图形的判断及有关证明.
抛物线中定点问题的解决方法:
在高考中一般以填空题或选择题的形式考查抛物线的定义、标准方程以及几何性质等基础知识,在解答题中常常将解析几何中的方法、技巧与思想集于一身,与其他圆锥曲线或其他章节的内容相结合,考查综合分析问题的能力,而与抛物线有关的定值及最值问题是一个很好的切人点,充分利用点在抛物线上及抛物线方程的特点是解决此类题型的关键,在求最值时经常运用基本不等式、判别式以及转化为函数最值等方法。
利用焦点弦求值:
利用抛物线及焦半径的定义,结合焦点弦的表示,进行有关的计算或求值。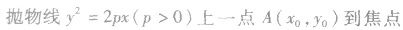
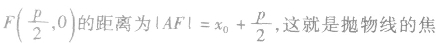
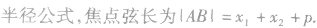
与“如图,设P是抛物线C1:x2=y上的动点.过点P做圆C2:x2+(y+3...”考查相似的试题有:
- (本题满分12分)已知函数f(x)=lnx-ax(a∈R)。(1)若函数f(x)单调递增,求实数a的取值范围;(2)当a>0时,求函数f(x)在[1,2]...
- 求曲线的斜率等于4的切线方程.
- 已知,如果过点可作曲线的三条切线,则m的取值范围是A.B.C.D.
- (本题满分10分)已知函数图象上的点处的切线方程为.(I)若函数在时有极值,求的表达式;(Ⅱ)函数在区间上单调递增,求实数...
- 设函数,当时,恒成立,则实数的取值范围是A.B.C.D.
- 已知函数f(x)=x3﹣3x,直线方程为y=ax+16,与曲线y=f(x)相切,则实数a的值是[ ]A.﹣3B.3C.6D.9
- (本小题满分13分)已知直线经过点A,求:(1)直线在两坐标轴上的截距相等的直线方程;(2)直线与两坐标轴的正向围成三角形...
- 过点A(1,-1)、B(-1,1)且圆心在直线x+y-2=0上的圆的方程是A.(x-3)2+(y+1)2=4B.(x+3)2+(y-1)2=4C.(x-1)2+(y-1)2=4D.(...
- 设抛物线y2=8x的准线与x轴交于点Q,若过点Q的直线l与抛物线有公共点,则直线l的斜率的取值范围是( )A.[-12,12]B.[-2,2]...
- 抛物线y=-12x2的焦点坐标是______.