本试题 “设命题p:实数x满足x2-4ax+3a2<0,其中a>0,命题q:实数x满足x2-x-6≤0x2+2x-8>0.若¬p是¬q的充分不必要条件,求实数a的取值范围.” 主要考查您对真命题、假命题
充分条件与必要条件
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 真命题、假命题
- 充分条件与必要条件
命题的概念:
1、命题:把语言、符号或式子表达的,可以判断真假的陈述句称为命题;
2、真命题、假命题:判断为真的语句称为真命题,判断为假的语句称为假命题。
注意:
1、并不是所有的语句都是命题,只有能够判断真假的语句才是命题。
2、如果一个语句是命题,则它是真命题或是假命题,二者必具其一。
1、充分条件与必要条件:一般地,“若p,则q”为真命题,是指由p通过推理可以得出q,这时,我们就说,由p可推出q,记作 ,并且说p是q的充分条件,q是p的必要条件;
,并且说p是q的充分条件,q是p的必要条件;
2、充要条件:一般地,如果既有 ,又有
,又有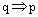 ,就记作
,就记作 ,此时,我们说,p是q的充分必要条件,简称充要条件。
,此时,我们说,p是q的充分必要条件,简称充要条件。
概括的说,如果 ,那么p与q互为充要条件。
,那么p与q互为充要条件。
3、充分不必要条件、必要不充分条件、既不充分也不必要条件:
①充分不必要条件:如果 ,且p
,且p q,则说p是q的充分不必要条件;
q,则说p是q的充分不必要条件;
②必要不充分条件:如果p q,且
q,且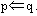 ,则说p是q的必要不充分条件;
,则说p是q的必要不充分条件;
③既不充分也不必要条件:如果p q,且p
q,且p q,则说p是q的既不充分也不必要条件。
q,则说p是q的既不充分也不必要条件。
发现相似题
与“设命题p:实数x满足x2-4ax+3a2<0,其中a>0,命题q:实数x满...”考查相似的试题有:
- 连结球面上两点的线段称为球的弦。半径为4的球的两条弦AB、CD的长度分别等于,M、N分别为AB、CD的中点,每条弦的两端都在球面...
- 下列命题中是假命题的是[ ]A.α,β∈R,使cos(α+β)=cosα+sinβB.x>0,有ln6x+ln3x+1>0C.上递减D.∈R,函数y=sin(2x+)都不是...
- 已知p:方程x2+mx+1=0有两个不等的负实根,q:方程4x2+4(m-2)+1=0无实根。若p或q 为真,p且q为假,求实数m的取值范围。
- 已知P:对任意a∈[1,2],不等式|m-5|≤a2+8恒成立; Q:函数f(x)=x3+mx2+mx+6x+1存在极大值和极小值.求使“P且¬Q”为真命题的...
- x+3>2是-x<6的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分又不必要条件
- 设是右焦点为的椭圆上三个不同的点,则“ 成等差数列”是“”的A.充要条件B.必要不充分条件C.充分不必要条件D.既非充分也非必要
- 若x,y∈R,则“x=0”是“x+yi为纯虚数”的( )A.充分不必要条件B.必要不充分条件C.充要条件D.不充分也不必要条件
- 若a∈R,则“a=1”是“|a|=1”的[ ]A、充分而不必要条件B、必要而不充分条件C、充要条件D、既不充分又不必要条件
- “存在实数λ,使a=λb成立”是“向量a和b共线”的[ ]A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件
- 已知平面上定点F1、F2及动点M,命题甲:命题乙:M点轨迹是以F1、F2为焦点的双曲线,则甲是乙的( )A.充分条件B.必要条件C...