本试题 “已知集合A={y|y=x2-x+1,x∈[,2]},B={x||x+m2|≥1},命题p:x∈A,命题q:x∈B,并且命题p是命题q的充分条件,求实数m的取值范围.” 主要考查您对集合间的基本关系
充分条件与必要条件
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 集合间的基本关系
- 充分条件与必要条件
集合与集合的关系有“包含”与“不包含”,“相等”三种:
1、 子集概念:
一般地,对于两个集合A与B,如果集合A的任何一个元素都是集合B的元素,就说集合B包含A,记作A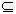 B(或说A包含于B),
B(或说A包含于B),
也可记为B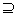 A(B包含A),此时说A是B的子集;A不是B的子集,记作A
A(B包含A),此时说A是B的子集;A不是B的子集,记作A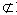 B,读作A不包含于B
B,读作A不包含于B
2、集合相等:
对于集合A和B,如果集合A中的每一个元素都是集合B的元素,反过来,集合B的每一个元素也都是集合A的元素,即集合A是集合B的子集,且集合B是集合A的子集,我么就说集合A和集合B相等,记作A=B
3、真子集:
对于集合A与B,如果A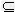 B并且A≠B,则集合A是集合B的真子集,记作A
B并且A≠B,则集合A是集合B的真子集,记作A B(B
B(B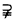 A),读作A真包含于B(B真包含A)
A),读作A真包含于B(B真包含A)
集合间基本关系:
性质1:
(1)空集是任何集合的子集,即A;
(2)空集是任何非空集合的真子集;
(3)传递性:AB,BCAC;AB,BCAC;
(4)AB,BAA=B。
性质2:
子集个数的运算:含n个元素的集合A的子集有2n个,非空子集有2n-1个,非空真子集有2n-2个。
集合间基本关系性质:
(1)空集是任何集合的子集,即A;
(2)空集是任何非空集合的真子集;
(3)传递性: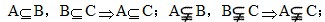
(4)集合相等:
(5)含n个元素的集合A的子集有2n个,非空子集有2n-1个,非空真子集有2n-2个。
1、充分条件与必要条件:一般地,“若p,则q”为真命题,是指由p通过推理可以得出q,这时,我们就说,由p可推出q,记作 ,并且说p是q的充分条件,q是p的必要条件;
,并且说p是q的充分条件,q是p的必要条件;
2、充要条件:一般地,如果既有 ,又有
,又有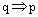 ,就记作
,就记作 ,此时,我们说,p是q的充分必要条件,简称充要条件。
,此时,我们说,p是q的充分必要条件,简称充要条件。
概括的说,如果 ,那么p与q互为充要条件。
,那么p与q互为充要条件。
3、充分不必要条件、必要不充分条件、既不充分也不必要条件:
①充分不必要条件:如果 ,且p
,且p q,则说p是q的充分不必要条件;
q,则说p是q的充分不必要条件;
②必要不充分条件:如果p q,且
q,且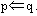 ,则说p是q的必要不充分条件;
,则说p是q的必要不充分条件;
③既不充分也不必要条件:如果p q,且p
q,且p q,则说p是q的既不充分也不必要条件。
q,则说p是q的既不充分也不必要条件。
与“已知集合A={y|y=x2-x+1,x∈[,2]},B={x||x+m2|≥1},命题p:x...”考查相似的试题有:
- 已知集合A={x|a2-2a≤x≤a+4},B={x|x2≤8x-7}。(1)若a=1,求集合(CRA)∩B;(2)若AB,求实数a的取值范围。
- 设非空集合M、N满足:M={x|f(x)=0},N={x|g(x)=0},P={x|f(x)g(x)=0},则集合P恒满足的关系为( ) A.P=M∪N B.P⊆(...
- 设命题:,命题:,若是的必要不充分条件,求实数的取值范围.
- 设A,B两点的坐标分别为(-1,0),(1,0).条件甲:A、B、C三点构成以∠C为钝角的三角形;条件乙:点C的坐标是方程x2+2y2=1...
- 已知p:>2,q:
- 已知命题p:12≤x≤1,命题q:x2-(2a+1)x+a(a+1)≤0,若¬p是¬q的必要而不充分条件,则实数a的取值范围是______.
- (1)是否存在实数m,使得2x+m<0是x2-2x-3>0的充分条件?(2)是否存在实数m,使得2x+m<0是x2-2x-3>0的必要条件?
- 已知p:x=3,q:x2-x-6=0,那么p是q的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件
- 已知p:x+1x-1≤0; q:lg(x+1+1-x2)有意义,则¬p是¬q的( ) 条件.A.充分不必要B.必要不充分C.充要条件D.既不充分也不必要
- “或”是“”的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件