本试题 “已知A、B两点的坐标分别为A(cosx2,sinx2),B(cos3x2,-sin3x2),其中x∈[-π2,0].(Ⅰ)求|AB|的表达式;(Ⅱ)若OA•OB=13(O为坐标原点),求tanx的值;(Ⅲ)...” 主要考查您对函数的单调性、最值
向量数量积的运算
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 函数的单调性、最值
- 向量数量积的运算
单调性的定义:
1、对于给定区间D上的函数f(x),若对于任意x1,x2∈D,当x1<x2时,都有f(x1)<f(x2),则称f(x)是区间上的增函数;当x1<x2时,都有f(x1)>f(x2),则称f(x)是区间D上的减函数。
2、如果函数y=f(x)在区间上是增函数或减函数,就说函数y=f(x)在区间D上具有(严格的)单调性,区间D称为函数f(x)的单调区间。如果函数y=f(x)在区间D上是增函数或减函数,区间D称为函数f(x)的单调增或减区间
3、最值的定义:
最大值:一般地,设函数y=f(x)的定义域为I,如果存在实数M,满足: ①对于任意的x∈I,都有f(x)≤M;②存在x0∈I,使得f(x0)=M;那么,称M是f(x)的最大值.
最小值:一般地,设函数y=f(x)的定义域为I,如果存在实数M,满足: ①对于任意的x∈I,都有f(x)≥M;②存在x0∈I,使得f(x0)=M;那么,称M是f(x)的最小值
判断函数f(x)在区间D上的单调性的方法:
(1)定义法:其步骤是:
①任取x1,x2∈D,且x1<x2;
②作差f(x1)-f(x2)或作商 ,并变形;
,并变形;
③判定f(x1)-f(x2)的符号,或比较 与1的大小;
与1的大小;
④根据定义作出结论。
(2)复合法:利用基本函数的单调性的复合。
(3)图象法:即观察函数在区间D上部分的图象从左往右看是上升的还是下降的。
两个向量数量积的含义:
如果两个非零向量 ,
, ,它们的夹角为
,它们的夹角为 ,我们把数量
,我们把数量 叫做
叫做 与
与 的数量积(或内积或点积),记作:
的数量积(或内积或点积),记作: ,即
,即 。
。 叫
叫 在
在 上的投影。
上的投影。
规定:零向量与任一向量的数量积是0,注意数量积是一个实数,不再是一个向量。
数量积的的运算律:
已知向量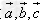 和实数λ,下面(1)(2)(3)分别叫做交换律,数乘结合律,分配律。
和实数λ,下面(1)(2)(3)分别叫做交换律,数乘结合律,分配律。
(1)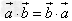 ;
;
(2)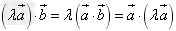 ;
;
(3)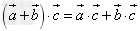 。
。
向量数量积的性质:
设两个非零向量
(1) ;
;
(2) ;
;
(3) ;
;
(4) ;
;
(5)当 ,
, 同向时,
同向时, ;当
;当 与
与 反向时,
反向时, ;当
;当 为锐角时,
为锐角时, 为正且
为正且 ,
, 不同向,
不同向, ;当
;当 为钝角时,
为钝角时, 为负且
为负且 ,
, 不反向,
不反向, 。
。
与“已知A、B两点的坐标分别为A(cosx2,sinx2),B(cos3x2,-sin3x...”考查相似的试题有:
- 已知函数f(x)=2x+2-x2,g(x)=2x-2-x2,(1)计算:[f(1)]2-[g(1)]2;(2)证明:[f(x)]2-[g(x)]2是定值.
- 下列各函数中在(0,2)上为增函数的是[ ]A.B.y=log2C.y=log3D.
- 设是奇函数,且在内是减函数,又,则的解集是
- 已知函数f(x)=2x+2ax+b,且f(1)=52,f(2)=174.(1)求a、b;(2)判断f(x)的奇偶性;(3)试判断函数在(-∞,0]上的...
- 定义在R上的函数f(x)满足f(x)=log2(1-x),x≤0f(x-1)-f(x-2),x>0,则f(2011)的值为( )A.-1B.0C.1D.2
- 下列四个命题:①定义在R上的函数f(x)满足f(-2)=f(2),则f(x)不是奇函数;②定义在R上的函数f(x)恒满足f(-x)=|f(x...
- 设函数f(x)=4x4x+2,那么f(111)+f(211)+…+f(1011)的值为______.
- 函数 的单调递增区间是
- 定义在R上的单调函数f(x)满足f(3)=log23且对任意x,y∈R都有f(x+y)=f(x)+f(y).(1)求证f(x)为奇函数;(2)若f...
- 已知|a|=3,|b|=23,a•b=-3,则a与b的夹角是( )A.30°B.60°C.120°D.150°