本试题 “在平面直角坐标系中,O为坐标原点,已知p=(-1,2),A(8,0),B(n,t),C(ksinθ,t),其中0≤θ≤π2(1)若AB⊥p,且|AB|=5|OA|,求向量OB;(2)若向量AC∥p...” 主要考查您对用数量积表示两个向量的夹角
用数量积判断两个向量的垂直关系
向量模的计算
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 用数量积表示两个向量的夹角
- 用数量积判断两个向量的垂直关系
- 向量模的计算
用数量积表示两个向量的夹角:
设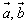 都是非零向量,
都是非零向量,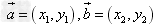 ,θ是
,θ是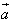 与
与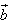 的夹角,根据向量数量积的定义及坐标表示可得
的夹角,根据向量数量积的定义及坐标表示可得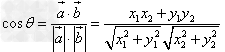 。
。
向量数量积问题中方法提炼:
(1)平面向量的数量积的运算有两种形式,一是依据定义来计算,二是利用坐标来计算,具体应用哪种形式应根据已知条件的特征来选择;
(2)平面向量数量积的计算类似于多项式的运算,解题中要注意多项式运算方法的运用;
(3)平面向量数量积的计算中要注意平面向量基本定理的应用,选择合适的基底,以简化运算
(4)向量的数量积是一个数而不是一个向量。
两向量垂直的充要条件:
非零向量 ,那么
,那么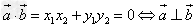 ,所以可以根据此公式判断两个向量是否垂直。
,所以可以根据此公式判断两个向量是否垂直。
向量数量积的性质:
设两个非零向量
(1) ;
;
(2) ;
;
(3) ;
;
(4) ;
;
(5)当 ,
, 同向时,
同向时, ;当
;当 与
与 反向时,
反向时, ;当
;当 为锐角时,
为锐角时, 为正且
为正且 ,
, 不同向,
不同向, ;当
;当 为钝角时,
为钝角时, 为负且
为负且 ,
, 不反向,
不反向, 。
。
向量的模:
设 ,则有向线段
,则有向线段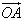 的长度叫做向量
的长度叫做向量 的长度或模,记作:
的长度或模,记作: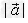 ,则
,则  。
。
向量模的坐标表示:
(1)若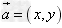 ,则
,则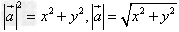 ;
;
(2)若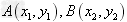 ,那么
,那么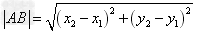 。
。
求向量的模:
求向量的模主要是利用公式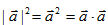 来解。
来解。
发现相似题
与“在平面直角坐标系中,O为坐标原点,已知p=(-1,2),A(8,0)...”考查相似的试题有:
- 已知a、b均为非零向量,命题p:a•b>0,命题q:a与b的夹角为锐角,则p是q成立的( )A.必要不充分条件B.充分不必要条件C....
- 已知a,b是非零向量且满足(a+2b)⊥a,(b+2a)⊥b,则a与b的夹角是______.
- 在△ABC中,若·>0,则角B的取值范围是( )A.(0,]B.(0,)C.[,π)D.(,π)
- 已知,是非零向量,且满足,。(1)求;(2)若,求与的夹角θ。
- 设x∈R,向量a=(x,1),b=(1,-2),且a⊥b,则|a+b|=______.
- 若与垂直,则k的值是( ) A.2 B.1 C.0 D.
- 已知点A(-1,-4),B(5,2),C(3,4),则下列结论正确的有______.①AC=(4,8)②|BC|=22③∠ABC=90°.
- 已知平面向量=(2,4),=(-2,2),若=+(·),则||等于( )A.6B.6C.6D.6
- 已知点A(1,0),B(0,1),C(2sinθ,cosθ)。(Ⅰ)若,求tanθ的值;(Ⅱ)若,其中O为坐标原点,求sin2θ的值。
- 向量均为单位向量,且,向量与向量的夹角为,则向量的模长的最大值为[ ]A.B.1C.D.2