本试题 “设a,b,c分别是△ABC的三个内角A,B,C所对应边的边长,若a=1,b=3,,A=30°是B=60°的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必...” 主要考查您对充分条件与必要条件
正弦定理
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 充分条件与必要条件
- 正弦定理
1、充分条件与必要条件:一般地,“若p,则q”为真命题,是指由p通过推理可以得出q,这时,我们就说,由p可推出q,记作 ,并且说p是q的充分条件,q是p的必要条件;
,并且说p是q的充分条件,q是p的必要条件;
2、充要条件:一般地,如果既有 ,又有
,又有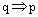 ,就记作
,就记作 ,此时,我们说,p是q的充分必要条件,简称充要条件。
,此时,我们说,p是q的充分必要条件,简称充要条件。
概括的说,如果 ,那么p与q互为充要条件。
,那么p与q互为充要条件。
3、充分不必要条件、必要不充分条件、既不充分也不必要条件:
①充分不必要条件:如果 ,且p
,且p q,则说p是q的充分不必要条件;
q,则说p是q的充分不必要条件;
②必要不充分条件:如果p q,且
q,且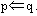 ,则说p是q的必要不充分条件;
,则说p是q的必要不充分条件;
③既不充分也不必要条件:如果p q,且p
q,且p q,则说p是q的既不充分也不必要条件。
q,则说p是q的既不充分也不必要条件。
正弦定理:
在一个三角形中,各边和它所对角的正弦的比相等,即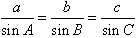 =2R。
=2R。
有以下一些变式:
(1)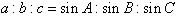 ;
;
(2)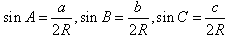 ;
;
(3)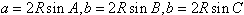 。
。
正弦定理在解三角形中的应用:
(1)已知两角和一边解三角形,只有一解。
(2)已知两边和其中一边的对角,解三角形,要注意对解的个数的讨论。可按如下步骤和方法进行:先看已知角的性质和已知两边的大小关系。
如已知a,b,A,
(一)若A为钝角或直角,当b≥a时,则无解;当a≥b时,有只有一个解;
(二)若A为锐角,结合下图理解。
①若a≥b或a=bsinA,则只有一个解。
②若bsinA<a<b,则有两解。
③若a<bsinA,则无解。 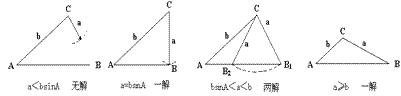
也可根据a,b的关系及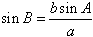 与1的大小关系来确定。
与1的大小关系来确定。
发现相似题
与“设a,b,c分别是△ABC的三个内角A,B,C所对应边的边长,若a=1...”考查相似的试题有:
- 给出以下命题:(1)函数y=f(x)的图象与直线x=2最多有一个交点;(2)当sinx≠0时,函数y=sin2x+4sin2x的最小值是4;(3)函...
- 给出如下三个命题:①若“p且q”为假命题,则p、q均为假命题;②命题“若x≥2且y≥3,则x+y≥5”的否命题为“若x<2且y<3,则x+y<5”;...
- 使复数为实数的充分而不必要条件是由 ( )A.B.C.为实数D.为实数
- “a=1”是“直线x+y=0和直线x-ay=0互相垂直”的( )A.充要条件B.必要而不充分条件C.充分而不必要条件D.既不充分也不必...
- “|x|<1”是“-3<x<1”成立的( )条件.A.既不充分也不必要B.充要C.必要不充分D.充分不必要
- 若p:x3-2x=x2,q:3-2x=x2,试讨论p是q的什么条件.
- 已知△ABC的一个内角为120°,并且三边长构成公差为4的等差数列,则△ABC的面积为153153.
- 设函数f(x)=,其中向量=(2cosx,1),=(cosx,sin2x),x∈R , (1)求f(x)的最小正周期与单调减区间;(2)在△ABC中,...
- 在△ABC中,已知∠A=30°,a,b分别为∠A,∠B的对边,且a=4=33b,解此三角形.
- 在中,角的对边分别为,且(1)求角的大小;(2) 若,求的面积.