本试题 “已知函数f(x)=13ax3+bx2+x+3,其中a≠0,则f(x)能取得极值的充要条件是______.” 主要考查您对充分条件与必要条件
函数的极值与导数的关系
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 充分条件与必要条件
- 函数的极值与导数的关系
1、充分条件与必要条件:一般地,“若p,则q”为真命题,是指由p通过推理可以得出q,这时,我们就说,由p可推出q,记作 ,并且说p是q的充分条件,q是p的必要条件;
,并且说p是q的充分条件,q是p的必要条件;
2、充要条件:一般地,如果既有 ,又有
,又有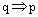 ,就记作
,就记作 ,此时,我们说,p是q的充分必要条件,简称充要条件。
,此时,我们说,p是q的充分必要条件,简称充要条件。
概括的说,如果 ,那么p与q互为充要条件。
,那么p与q互为充要条件。
3、充分不必要条件、必要不充分条件、既不充分也不必要条件:
①充分不必要条件:如果 ,且p
,且p q,则说p是q的充分不必要条件;
q,则说p是q的充分不必要条件;
②必要不充分条件:如果p q,且
q,且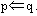 ,则说p是q的必要不充分条件;
,则说p是q的必要不充分条件;
③既不充分也不必要条件:如果p q,且p
q,且p q,则说p是q的既不充分也不必要条件。
q,则说p是q的既不充分也不必要条件。
极值的定义:
(1)极大值: 一般地,设函数f(x)在点x0附近有定义,如果对x0附近的所有的点,都有f(x)<f(x0),就说f(x0)是函数f(x)的一个极大值,记作y极大值=f(x0),x0是极大值点;
(2)极小值:一般地,设函数f(x)在x0附近有定义,如果对x0附近的所有的点,都有f(x)>f(x0),就说f(x0)是函数f(x)的一个极小值,记作y极小值=f(x0),x0是极小值点。
极值的性质:
(1)极值是一个局部概念,由定义知道,极值只是某个点的函数值与它附近点的函数值比较是最大或最小,并不意味着它在函数的整个的定义域内最大或最小;
(2)函数的极值不是唯一的,即一个函数在某区间上或定义域内极大值或极小值可以不止一个;
(3)极大值与极小值之间无确定的大小关系,即一个函数的极大值未必大于极小值;
(4)函数的极值点一定出现在区间的内部,区间的端点不能成为极值点,而使函数取得最大值、最小值的点可能在区间的内部,也可能在区间的端点。
判别f(x0)是极大、极小值的方法:
若x0满足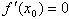 ,且在x0的两侧f(x)的导数异号,则x0是f(x)的极值点,
,且在x0的两侧f(x)的导数异号,则x0是f(x)的极值点, 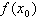 是极值,并且如果
是极值,并且如果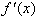 在x0两侧满足“左正右负”,则x0是f(x)的极大值点,f(x0)是极大值;如果
在x0两侧满足“左正右负”,则x0是f(x)的极大值点,f(x0)是极大值;如果 在x0两侧满足“左负右正”,则x0是f(x)的极小值点,f(x0)是极小值。
在x0两侧满足“左负右正”,则x0是f(x)的极小值点,f(x0)是极小值。
求函数f(x)的极值的步骤:
(1)确定函数的定义区间,求导数f′(x);
(2)求方程f′(x)=0的根;
(3)用函数的导数为0的点,顺次将函数的定义区间分成若干小开区间,并列成表格,检查f′(x)在方程根左右的值的符号,如果左正右负,那么f(x)在这个根处取得极大值;如果左负右正,那么f(x)在这个根处取得极小值;如果左右不改变符号即都为正或都为负,则f(x)在这个根处无极值。
对函数极值概念的理解:
极值是一个新的概念,它是研究函数在某一很小区域时给出的一个概念,在理解极值概念时要注意以下几点:
①按定义,极值点x0是区间[a,b]内部的点,不会是端点a,b(因为在端点不可导).如图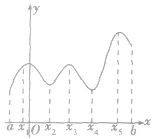
②极值是一个局部性概念,只要在一个小领域内成立即可.要注意极值必须在区间内的连续点取得.一个函数在定义域内可以有许多个极小值和极大值,在某一点的极小值也可能大于另一个点的极大值,也就是说极大值与极小值没有必然的大小关系,即极大值不一定比极小值大,极小值不一定比极大值小,如图.
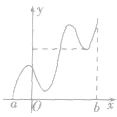
③若fx)在(a,b)内有极值,那么f(x)在(a,b)内绝不是单调函数,即在区间上单调的函数没有极值.
④若函数f(x)在[a,b]上有极值且连续,则它的极值点的分布是有规律的,相邻两个极大值点之间必有一个极小值点,同样相邻两个极小值点之间必有一个极大值点,一般地,当函数f(x)在[a,b]上连续且有有
限个极值点时,函数f(x)在[a,b]内的极大值点、极小值点是交替出现的,
⑤可导函数的极值点必须是导数为0的点,但导数为0的点不一定是极值点,不可导的点也可能是极值点,也可能不是极值点,
与“已知函数f(x)=13ax3+bx2+x+3,其中a≠0,则f(x)能取得极值的充...”考查相似的试题有:
- 用分析法证明:欲使①A>B,只需②C<D,这里①是②的( )A.充分条件B.必要条件C.充要条件D.既不充分也不必要条件
- 已知p:直线a与平面α内无数条直线垂直,q:直线a与平面α垂直,则p是q的( )条件。(用“充分不必要”、“必要不充分”、“充要”、...
- “|x|<1”是“<0”的A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件
- 记实数x1,x2,…xn中的最大数为max{x1,x2,…xn},最小数为min{x1,x2,…xn}.已知△ABC的三边边长为a、b、c(a≤b≤c),定义它...
- 如果对于任意实数x,[x]表示不超过x的最大整数.例如[3.27]=3,[0.6]=0.那么“[x]=[y]”是“|x-y|<1”的( )A.充分而不必要条...
- 若limn→∞(41-a+4a1-a+4a21-a+…+4an-11-a)=9,则实数a等于( )A.53B.13C.-53D.-13
- 若以曲线y=f(x)任意一点M(x,y)为切点作切线l,曲线上总存在异于M的点N(x1y1),以点N为切点作切线l1,且l∥l1,则称曲线...
- 已知函数f(x)=ax2+2ln(2-x)(a∈R),设曲线y=f(x)在点(1,f(1))处的切线为l,若l与圆C:x2+y2=14相切,求a的值.
- 设x1,x2分别是函数f(x)=﹣2x3+3(1﹣2a)x2+12ax﹣1的极小值点和极大值点.已知=x2,求a的值及函数的极值.
- limx→+∞(12)x=( )A.0B.12C.1D.不存在