本试题 “已知函数f(x)=sinx+cosx,f'(x)是f(x)的导函数(1)当x∈[0,π2]时求函数g(x)=f(x)f′(x)+f2(x)的值域.(2)在直角坐标系中画出y=g(x)-1在[-π2,π2]上的...” 主要考查您对函数的定义域、值域
函数图象
导数的运算
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 函数的定义域、值域
- 函数图象
- 导数的运算
定义域、值域的概念:
自变量取值范围叫做函数的定义域,函数值的集合叫做函数的值域。
1、求函数定义域的常用方法有:
(1)根据解析式要求如偶次根式的被开方大于零,分母不能为零等;
(2)根据实际问题的要求确定自变量的范围;
(3)根据相关解析式的定义域来确定所求函数自变量的范围;
(4)复合函数的定义域:如果y是u的函数,而u是x的函数,即y=f(u),u=g(x),那么y=f[g(x)]叫做函数f与g的复合函数,u叫做中间变量,设f(x)的定义域是x∈M,g(x)的定义域是x∈N,求y=f[g(x)]的定义域时,则只需求满足 的x的集合。设y=f[g(x)]的定义域为P,则
的x的集合。设y=f[g(x)]的定义域为P,则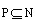 。
。
3、求函数值域的方法:
(1)利用一些常见函数的单调性和值域,如一次函数,二次函数,反比例函数,指数函数,对数函数,三角函数,形如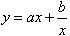 (a,b为非零常数)的函数;
(a,b为非零常数)的函数;
(2)利用函数的图象即数形结合的方法;
(3)利用均值不等式;
(4)利用判别式;
(5)利用换元法(如三角换元);
(6)分离法:分离常数与分离参数两种形式;
(7)利用复合函数的单调性。(注:二次函数在闭区间上的值域要特别注意对称轴与闭区间的位置关系,含字母时要注意讨论)
定义:
点集{(x,y)|y=f(x)}叫做函数y=f(x)的图像。
函数图像的画法:
(1)描点法:
一般我们选择一些特殊点(包括区间端点、最值点、极值点、函数图像与坐标轴的交点等)。
(2)用函数的性质画图
一般我们选择先确定函数的定义域,再看函数是否具有周期性和对称性、奇偶性,这样我们就可以只画出部分图像,之后根据性质直接得到其余部分的图像,然后判断单调性,确定特殊点或渐近线,进而得到函数的大致图像。
(3)通过图像变换画图
(一)平移变化:
Ⅰ水平平移:函数y=f(x+a)的图像可以把函数y=f(x)的图像沿x轴方向向左(a>0)或向右(a<0)平移|a|个单位即可得到;
Ⅱ竖直平移:函数y=f(x+a)的图像可以把函数y=f(x)的图像沿x轴方向向上(a>0)或向下(a<0)平移|a|个单位即可得到.
(二)对称变换:
Ⅰ函数y=f(-x)的图像可以将函数y=f(x)的图像关于y轴对称即可得到;
Ⅱ函数y=-f(x)的图像可以将函数y=f(x)的图像关于x轴对称即可得到;
Ⅲ函数y=-f(-x)的图像可以将函数y=f(x)的图像关于原点对称即可得到;
Ⅳ函数y=f-1(x)的图像可以将函数y=f(x)的图像关于直线y=x对称得到.
函数图像的判断:
这里主要是抽象函数的图像,借助函数的对称性、周期性及单调性确定函数的图像;另外借助导数,就是函数在某点处的切线斜率的变化,体现在函数的图像上就是增长的快还是慢来确定函数的图像。
常用结论:
(1)若函数y=f(x)定义域内任一x的值都满足f(a+x)=f(b-x),则y=f(x)的图像关于直线 成轴对称图形;特别地,y=f(x)满足
成轴对称图形;特别地,y=f(x)满足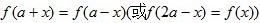 恒成立,则y=f(x)的图像关于直线x=a成轴对称图形;
恒成立,则y=f(x)的图像关于直线x=a成轴对称图形;
(2)函数y=f(x)的图像关于直线x=a及x=b对称,则y=f(x)是周期函数,且2|b-a|是它的一个周期。
常见函数的导数:
(1)C′=0 ;(2)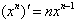 ;(3)
;(3)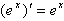 ;(4)
;(4) ;(5)
;(5)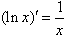 ;(6)
;(6)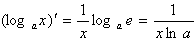 ;(7)
;(7)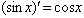 ;(8)
;(8)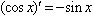
导数的四则运算:
(1)和差: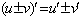
(2)积: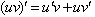
(3)商:
复合函数的导数:
运算法则复合函数导数的运算法则为: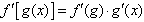
复合函数的求导的方法和步骤:
(1)分清复合函数的复合关系,选好中间变量;
(2)运用复合函数求导法则求复合函数的导数,注意分清每次是哪个变量对哪个变量求导数;
(3)根据基本函数的导数公式及导数的运算法则求出各函数的导数,并把中间变量换成自变量的函数。
求复合函数的导数一定要抓住“中间变量”这一关键环节,然后应用法则,由外向里一层层求导,注意不要漏层。
与“已知函数f(x)=sinx+cosx,f'(x)是f(x)的导函数(1)当x...”考查相似的试题有:
- 函数的定义域是 .
- 设,g(x)=ax+5﹣2a(a>0).(1)求f(x)在x∈[0,1]上的值域;(2)若对于任意x1∈[0,1],总存在x0∈[0,1],使得g(x0)=...
- 设函数f(x)=x3+ax2+bx(x>0)的图象与直线y=4相切于M(1,4)。(Ⅰ)求f(x)=x3+ax2+bx在区间(0,4]上的最大值与最小值;(Ⅱ)设...
- 函数的定义域是 A.B.C.D.
- 已知函数,(Ⅰ)求函数的定义域;(Ⅱ)求函数的单调区间;(Ⅲ)当>0时,若存在x使得成立,求的取值范围.
- 已知在定义域R上是减函数,则函数y=f (|x+2|)的单调递增区间是( )A.(-∞, +∞) B.(2, +∞) C.(-2, +∞) D(―∞, ―2)
- 设函数f(x)=x|x|,将f(x)向左平移a(a>0)个单位得到函数g(x),将f(x)向上平移a(a>0)个单位得到函数h(x),若g...
- 为了得到函数y=lgx10的图象,只需把函数y=lgx的图象上( )A.所有点向右平移1个单位长度B.所有点向下平移1个单位长度C.所...
- (本小题满分14分)已知函数 (1)当时, 证明: 不等式恒成立;(2)若数列满足,证明数列是等比数列,并求出数列、的通项公式;(3)在...
- 已知函数f(x)=x2sinx,则f′(π2)等于______.