本试题 “已知数列{an}与数列{bn}(n∈N*,n≥1)满足:①a1<0,b1>0;②当k≥2时,ak与bk满足如下条件:当≥0时,ak=ak-1,;当<0时,,bk=bk-1,求:(1)用a1,b1表示bn...” 主要考查您对一般数列的通项公式
指数、对数不等式
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 一般数列的通项公式
- 指数、对数不等式
一般数列的定义:
如果数列{an}的第n项an与序号n之间的关系可以用一个式子表示成an=f(n),那么这个公式叫做这个数列的通项公式。
通项公式的求法:
(1)构造等比数列:凡是出现关于后项和前项的一次递推式都可以构造等比数列求通项公式;
(2)构造等差数列:递推式不能构造等比数列时,构造等差数列;
(3)递推:即按照后项和前项的对应规律,再往前项推写对应式。
已知递推公式求通项常见方法:
①已知a1=a,an+1=qan+b,求an时,利用待定系数法求解,其关键是确定待定系数λ,使an+1 +λ=q(an+λ)进而得到λ。
②已知a1=a,an=an-1+f(n)(n≥2),求an时,利用累加法求解,即an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)的方法。
③已知a1=a,an=f(n)an-1(n≥2),求an时,利用累乘法求解。
指数、对数不等式:
当a>1时, 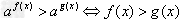 ;
; 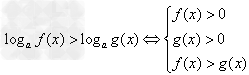
2、当0<a<1时, 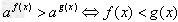 ;
; 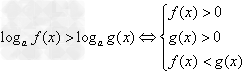 。
。
指数对数不等式的解法:
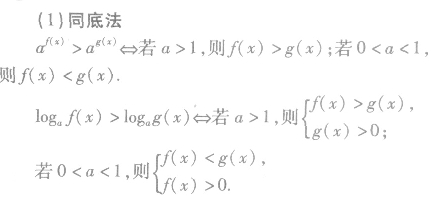
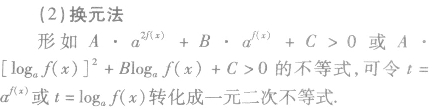
发现相似题
与“已知数列{an}与数列{bn}(n∈N*,n≥1)满足:①a1<0,b1>0;②...”考查相似的试题有:
- 已知数列{an}的前n项和为Sn,且满足:a1=a(a≠0),an+1=rSn(n∈N*,r∈R,r≠-1),(1)求数列{an}的通项公式;(2)若存在k∈N*,使得...
- 在数列{an}中,已知a1=2,an+1=an+cn(c是常数,n∈N*),且a1,a2,a3成公比不为1的等比数列,则{an}的通项公式是( )。
- 已知数列它的一个通项公式( )
- 设,,,则数列的通项公式是( )。
- 不等式的解集是 .
- 从社会效益和经济效益出发,某地投入资金进行生态环境建设,并以此发展旅游产业.根据规划,本年度投入800万元,以后每年投入...
- 设是满足不等式≥的自然数的个数.(1)求的函数解析式;(2),求;(3)设,由(2)中及构成函数,,求的最小值与最大值.(...
- 函数y=f(x)在区间(0,+∞)内可导,导函数f'(x)是减函数,且f′(x)>0。设x0∈(0,+∞),y=kx+m是曲线y=f(x)在点(x0...
- 不等式<4的解集是( )。
- 若不等式|3x-log13(x-2)|<3x+|log13(x-2)|成立,则x的范围是______.