本试题 “给出定义在(0,+∞)上的三个函数:f(x)=lnx,g(x)=x2﹣mf(x),,已知g(x)在x=1处取极值.(1)求m的值及函数h(x)的单调区间;(2)求证:当x∈(1...” 主要考查您对函数的单调性与导数的关系
综合法与分析法证明不等式
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 函数的单调性与导数的关系
- 综合法与分析法证明不等式
导数和函数的单调性的关系:
(1)若f′(x)>0在(a,b)上恒成立,则f(x)在(a,b)上是增函数,f′(x)>0的解集与定义域的交集的对应区间为增区间;
(2)若f′(x)<0在(a,b)上恒成立,则f(x)在(a,b)上是减函数,f′(x)<0的解集与定义域的交集的对应区间为减区间。
利用导数求解多项式函数单调性的一般步骤:
①确定f(x)的定义域;
②计算导数f′(x);
③求出f′(x)=0的根;
④用f′(x)=0的根将f(x)的定义域分成若干个区间,列表考察这若干个区间内f′(x)的符号,进而确定f(x)的单调区间:f′(x)>0,则f(x)在对应区间上是增函数,对应区间为增区间;f′(x)<0,则f(x)在对应区间上是减函数,对应区间为减区间。
函数的导数和函数的单调性关系特别提醒:
若在某区间上有有限个点使f′(x)=0,在其余的点恒有f′(x)>0,则f(x)仍为增函数(减函数的情形完全类似).即在区间内f′(x)>0是f(x)在此区间上为增函数的充分条件,而不是必要条件。
综合法:
利用某些已知的不等式或已证过的不等式或不等式的性质推导出所要证的不等式成立,这种证明方法叫综合法,即由因导果。利用均值不等式的有关公式最为常见。
分析法:
(1)从求证的不等式出发,分析使这个不等式成立的充分条件,把证明这个不等式的问题转化为这些条件是否具备的问题,如果能肯定这些条件都已具备,那么就可以判定所证的不等式成立,这种证明方法叫分析法,即执果索因;
(2)用分析法证明要注意格式:“若A成立,则B成立”的模式是:欲证B为真,只需证C为真,只需证D为真…最后得出A或已知的性质、公理、定理,从而得出B为真。也可使用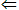 简化叙述。即B
简化叙述。即B C
C D
D …
… A或已知的性质、公理、定理。切不可使用B
A或已知的性质、公理、定理。切不可使用B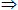 C
C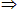 D
D …
…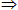 A。
A。
用综合法分析法证明不等式常用到的结论:

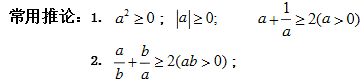
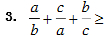 3,
3,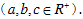
与“给出定义在(0,+∞)上的三个函数:f(x)=lnx,g(x)=x2﹣m...”考查相似的试题有:
- (本小题满分12分)已知函数在处取到极值2(Ⅰ)求的解析式;(Ⅱ)设函数.若对任意的,总存在唯一的,使得,求实数的取值范围....
- 若y=ax与y=-bx在(0,+∞)上都是减函数,对函数y=ax3+bx的单调性描述正确的是( )A.在(-∞,+∞)上是增函数B.在(0,+∞)...
- 已知函数f(x)=12x2-(a+1)x+alnx.(I)若曲线f(x)在点(2,f(2))处的切线与直线2x+3y+1=0垂直,求a的值;(II)讨论函数...
- f(x)是定义在(0,+∞)上的非负可导函数,且满足xf′(x)+f(x)≤0,对任意正数a、b,若a<b,则必有( )A.af(b)≤bf(a...
- 已知函数f(x)=kx2+(3+k)x+3,其中k为常数,且k≠0.(1)若f(2)=3,求函数f(x)的表达式;(2)在(1)的条件下,设函...
- 设f'(x)是函数f(x)的导函数,f'(x)的图象如图所示,则f(x)的图象最有可能是[ ]A.B.C.D.
- 已知函数f(x)=ax4lnx+bx4-c(x>0)在x=1处取得极值-3-c,其中a,b,c为常数。(1)试确定a,b的值;(2)讨论函数f(x)的单调区...
- 定义域R的奇函数f(x),当x∈(-∞,0)时f(x)+xf'(x)<0恒成立,若a=3f(3),b=f(1),c=-2f(-2),则( )A.a>c>b...
- 设函数f(x)=ax3+bx+cx+d的图象与y轴的交点为点P,且曲线在点P处的切线方程为12x-y-4=0,若函数在x=2处取得极值0,试求函数...
- 已知函数(且)恰有一个极大值点和一个极小值点,且其中一个极值点是(1)求函数的另一个极值点;(2)设函数的极大值为M,极...